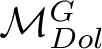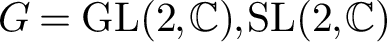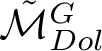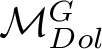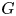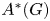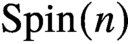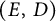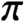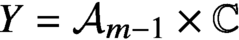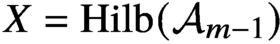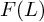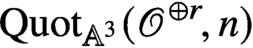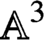Refine listing
Actions for selected content:
265 results in 14Cxx
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological invariants of root stacks and admissible double coverings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 November 2021, pp. 202-224
- Print publication:
- February 2023
-
- Article
- Export citation
Free quotients of fundamental groups of smooth quasi-projective varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 27 October 2021, pp. 924-946
-
- Article
- Export citation
Algebraic cycles and Lehn–Lehn–Sorger–van Straten eightfolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 04 October 2021, pp. 884-907
-
- Article
- Export citation
Infinitesimal structure of the pluricanonical double ramification locus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2280-2337
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic cycles and intersections of three quadrics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 349-367
- Print publication:
- September 2022
-
- Article
- Export citation
De Rham–Witt sheaves via algebraic cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 2089-2132
- Print publication:
- October 2021
-
- Article
- Export citation
INTERSECTION COHOMOLOGY OF THE MODULI SPACE OF HIGGS BUNDLES ON A GENUS 2 CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 02 August 2021, pp. 1037-1086
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
P = W for Lagrangian fibrations and degenerations of hyper-Kähler manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 25 June 2021, e50
-
- Article
-
- You have access
- Open access
- Export citation
On the Chow ring of some special Calabi–Yau varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 308-327
- Print publication:
- June 2022
-
- Article
- Export citation
Hopf-theoretic approach to motives of twisted flag varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 963-996
- Print publication:
- May 2021
-
- Article
- Export citation
Maximal indexes of flag varieties for spin groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 April 2021, e34
-
- Article
-
- You have access
- Open access
- Export citation
On certain Tannakian categories of integrable connections over Kähler manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1034-1061
- Print publication:
- August 2022
-
- Article
- Export citation
Quasimaps and stable pairs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 12 April 2021, e32
-
- Article
-
- You have access
- Open access
- Export citation
A support theorem for Hilbert schemes of planar curves, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 28 April 2021, pp. 835-882
- Print publication:
- April 2021
-
- Article
- Export citation
ON THE CHOW RING OF CERTAIN LEHN–LEHN–SORGER–VAN STRATEN EIGHTFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 22 March 2021, pp. 253-276
-
- Article
- Export citation
RECIPROCITY SHEAVES AND THEIR RAMIFICATION FILTRATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 19 March 2021, pp. 71-144
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
Higher rank K-theoretic Donaldson-Thomas Theory of points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 March 2021, e15
-
- Article
-
- You have access
- Open access
- Export citation
Rigid-analytic varieties with projective reduction violating Hodge symmetry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 625-640
- Print publication:
- March 2021
-
- Article
- Export citation
Log
 $\mathscr{D}$-modules and index theorems
$\mathscr{D}$-modules and index theorems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e3
-
- Article
-
- You have access
- Open access
- Export citation