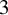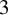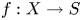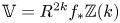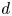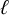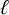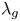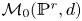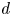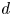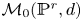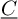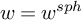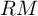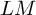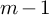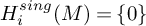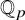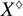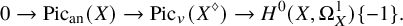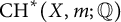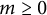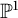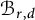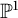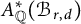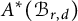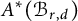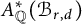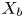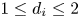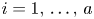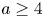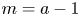Refine listing
Actions for selected content:
262 results in 14Cxx
On the effective, nef, and semi-ample monoids of blowups of Hirzebruch surfaces at collinear points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1179-1193
- Print publication:
- December 2023
-
- Article
- Export citation
Extremal Gromov-Witten invariants of the Hilbert scheme of
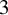 $3$ Points
$3$ Points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 March 2023, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sets of special subvarieties of bounded degree
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 14 March 2023, pp. 616-657
- Print publication:
- March 2023
-
- Article
- Export citation
Noninjectivity of the cycle class map in continuous
 $\ell $-adic cohomology
$\ell $-adic cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 February 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reciprocity sheaves and logarithmic motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. 355-379
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hodge bundle, the universal 0-section, and the log Chow ring of the moduli space of curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 306-354
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived categories of hyper-Kähler manifolds: extended Mukai vector and integral structure
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 109-152
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The integral Chow ring of
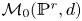 $\mathcal {M}_{0}(\mathbb {P}^r, d)$, for
$\mathcal {M}_{0}(\mathbb {P}^r, d)$, for 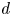 $d$ odd
$d$ odd
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 184-206
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute Poincaré duality in étale cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 November 2022, e99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MORPHISMS KILLING WEIGHTS AND STABLE HUREWICZ-TYPE THEOREMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 October 2022, pp. 521-556
- Print publication:
- March 2024
-
- Article
- Export citation
LAURICELLA HYPERGEOMETRIC FUNCTIONS, UNIPOTENT FUNDAMENTAL GROUPS OF THE PUNCTURED RIEMANN SPHERE, AND THEIR MOTIVIC COACTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 148-220
- Print publication:
- March 2023
-
- Article
- Export citation
Line bundles on rigid spaces in the v-topology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 September 2022, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double nested Hilbert schemes and the local stable pairs theory of curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 11 October 2022, pp. 1799-1849
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the cohomology of reciprocity sheaves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 August 2022, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deligne-Beilinson cohomology of the universal K3 surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 August 2022, e64
-
- Article
- Export citation
The six-functor formalism for rigid analytic motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 August 2022, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The complexity of higher Chow groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 29 July 2022, pp. 903-911
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The intersection theory of the moduli stack of vector bundles on
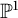 $\mathbb {P}^1$
$\mathbb {P}^1$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 359-379
- Print publication:
- June 2023
-
- Article
- Export citation
On birationally trivial families and adjoint quadrics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 04 July 2022, pp. 587-617
-
- Article
- Export citation
The logarithmic Picard group and its tropicalization
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 09 September 2022, pp. 1477-1562
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation