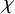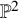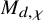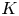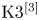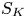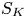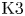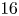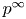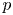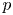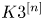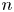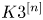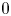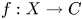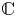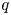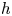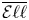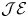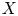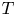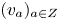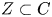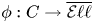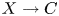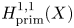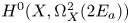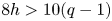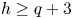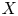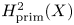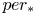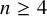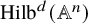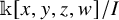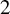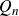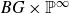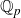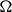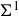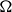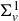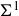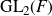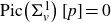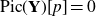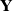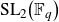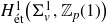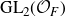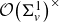Refine listing
Actions for selected content:
262 results in 14Cxx
Higher Chow cycles on a family of Kummer surfaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological
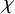 $\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on
$\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on 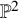 $\mathbb {P}^2$
$\mathbb {P}^2$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 01 April 2024, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sixfolds of generalized Kummer type and K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 388-410
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundedness of the p-primary torsion of the Brauer group of an abelian variety
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 463-480
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Families of rational curves on holomorphic symplectic varieties and applications to 0-cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 288-316
- Print publication:
- February 2024
-
- Article
- Export citation
On the nilpotent orbit theorem of complex variations of Hodge structure
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 November 2023, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ENDOMORPHISMS OF EXTENSIONS IN TANNAKIAN CATEGORIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 07 November 2023, pp. 103-114
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double Schubert polynomials do have saturated Newton polytopes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 November 2023, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of subpencils for hyperplane sections on certain K3 surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1022-1043
-
- Article
- Export citation
Generic Torelli and local Schottky theorems for Jacobian elliptic surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 06 October 2023, pp. 2521-2550
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ANTI-CANONICAL GEOMETRY OF WEAK
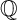 $\mathbb {Q}$-FANO THREEFOLDS, III
$\mathbb {Q}$-FANO THREEFOLDS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 23-47
- Print publication:
- March 2024
-
- Article
- Export citation
On the period of Li, Pertusi, and Zhao’s symplectic variety
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1432-1453
- Print publication:
- August 2024
-
- Article
- Export citation
On the strict Picard spectrum of commutative ring spectra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1872-1897
- Print publication:
- September 2023
-
- Article
- Export citation
On Bloch’s map for torsion cycles over non-closed fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 June 2023, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Refined unramified cohomology of schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1466-1530
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small elementary components of Hilbert schemes of points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 June 2023, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral Fourier transforms and the integral Hodge conjecture for one-cycles on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1188-1213
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coniveau filtrations and Milnor operation
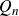 $Q_n$
$Q_n$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 08 May 2023, pp. 521-538
- Print publication:
- November 2023
-
- Article
- Export citation
The Picard group of vertex affinoids in the first Drinfeld covering
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 13 April 2023, pp. 423-432
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Log Product Formula in Quantum K-theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 225-252
- Print publication:
- September 2023
-
- Article
- Export citation