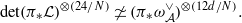Refine listing
Actions for selected content:
258 results in 14Cxx
The resolution property of algebraic surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 209-226
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Picard groups of punctured spectra of dimension three local hypersurfaces are torsion-free
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 145-152
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Pseudoeffective and nef classes on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 1793-1818
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
ℤ[1/p]-motivic resolution of singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 1434-1446
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Green’s conjecture for curves on arbitrary K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 839-851
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Norm functors and effective zero cycles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 557-574
-
- Article
-
- You have access
- Export citation
Motives of Azumaya algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 14 April 2010, pp. 481-599
- Print publication:
- July 2010
-
- Article
- Export citation
On Cox rings of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 964-998
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Rigid local systems and motives of type G2. With an appendix by Michale Dettweiler and Nicholas M. Katz
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 24 March 2010, pp. 929-963
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Algebraic cycles on the relative symmetric powers and on the relative Jacobian of a family of curves. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 23 March 2010, pp. 799-846
- Print publication:
- October 2010
-
- Article
- Export citation
Néron models and limits of Abel–Jacobi mappings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 02 February 2010, pp. 288-366
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Characteristic varieties and logarithmic differential 1-forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 129-144
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Produit eulérien motivique et courbes rationnelles sur les variétés toriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1360-1400
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
Algebraic and topological aspects of the schematization functor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 633-686
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
ON THE INTERSECTION OF RATIONAL TRANSVERSAL SUBTORI
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 221-231
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Schematic homotopy types and non-abelian Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 582-632
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
On the determinant bundles of abelian schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 495-502
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Hodge cycles on Kuga fiber varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-13
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
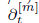 and ∂
and ∂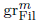 as multiplication by
as multiplication by 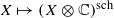 , introduced by the third author as a substitute for the rationalization functor in homotopy theory in the case of non-simply connected spaces. Our main result is the construction of a
, introduced by the third author as a substitute for the rationalization functor in homotopy theory in the case of non-simply connected spaces. Our main result is the construction of a 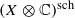 . This Hodge decomposition is encoded in an action of the discrete group
. This Hodge decomposition is encoded in an action of the discrete group 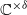 on the object
on the object 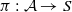 be an abelian scheme over a scheme
be an abelian scheme over a scheme 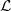 be a symmetric, rigidified, relatively ample line bundle on
be a symmetric, rigidified, relatively ample line bundle on 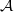 . We show that there is an isomorphism
. We show that there is an isomorphism 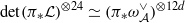
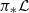 . We also show that the numbers 24 and 12
. We also show that the numbers 24 and 12