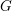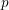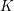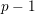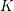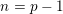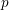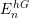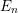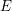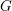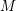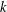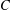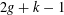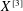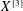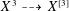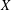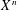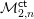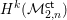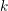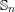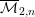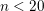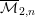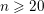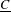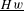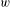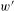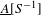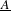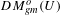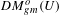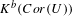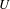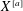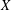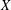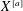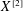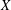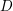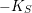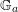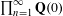Refine listing
Actions for selected content:
258 results in 14Cxx
HYPERELLIPTIC GRAPHS ANDMETRIZED COMPLEXES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 30 August 2017, e20
-
- Article
-
- You have access
- Open access
- Export citation
Équivalence motivique des groupes algébriques semisimples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 2195-2213
- Print publication:
- October 2017
-
- Article
- Export citation
Picard groups of higher real
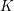 $K$ -theory spectra at height
$K$ -theory spectra at height 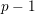 $p-1$
$p-1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1820-1854
- Print publication:
- September 2017
-
- Article
- Export citation
Construction of automorphisms of hyperkähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 1610-1621
- Print publication:
- August 2017
-
- Article
- Export citation
On descending cohomology geometrically
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 10 May 2017, pp. 1446-1478
- Print publication:
- July 2017
-
- Article
- Export citation
SOME NEW EXAMPLES OF SMASH-NILPOTENT ALGEBRAIC CYCLES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 623-634
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
On Teter rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 125-139
- Print publication:
- February 2017
-
- Article
- Export citation
A LOWER BOUND FOR THE GONALITY CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 03 April 2017, pp. 561-563
- Print publication:
- 2017
-
- Article
- Export citation
Chern–Schwartz–MacPherson classes for Schubert cells in flag manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 14 November 2016, pp. 2603-2625
- Print publication:
- December 2016
-
- Article
- Export citation
An approach to intersection theory on singular varieties using motivic complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 2371-2404
- Print publication:
- November 2016
-
- Article
- Export citation
THE MOTIVE OF THE HILBERT CUBE
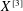 $X^{[3]}$
$X^{[3]}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 27 October 2016, e30
-
- Article
-
- You have access
- Open access
- Export citation
DYNAMICS ON SUPERSINGULAR K3 SURFACES AND AUTOMORPHISMS OF SALEM DEGREE 22
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 1-15
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
MIXED HODGE STRUCTURES OF THE MODULI SPACES OF PARABOLIC CONNECTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 225 / March 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 185-206
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
ALBANESE VARIETIES OF CYCLIC COVERS OF THE PROJECTIVE PLANE AND ORBIFOLD PENCILS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 05 October 2016, pp. 189-213
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
Tautological rings of spaces of pointed genus two curves of compact type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 17 June 2016, pp. 1398-1420
- Print publication:
- July 2016
-
- Article
- Export citation
NON-COMMUTATIVE LOCALIZATIONS OF ADDITIVE CATEGORIES AND WEIGHT STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 4 / September 2018
- Published online by Cambridge University Press:
- 24 May 2016, pp. 785-821
- Print publication:
- September 2018
-
- Article
- Export citation
THE INTEGRAL COHOMOLOGY OF THE HILBERT SCHEME OF TWO POINTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 27 April 2016, e8
-
- Article
-
- You have access
- Open access
- Export citation
Cylinders in singular del Pezzo surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 21 April 2016, pp. 1198-1224
- Print publication:
- June 2016
-
- Article
- Export citation
ADJOINT FUNCTORS ON THE DERIVED CATEGORYOF MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 March 2016, pp. 489-507
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
ULRICH IDEALS AND MODULES OVER TWO-DIMENSIONAL RATIONAL SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 69-110
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation