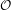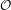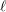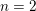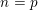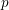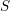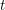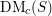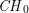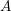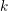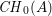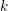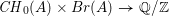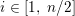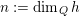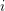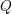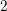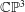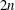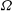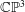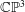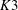Refine listing
Actions for selected content:
258 results in 14Cxx
Homaloidal nets and ideals of fat points I
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 54-77
-
- Article
-
- You have access
- Export citation
PERVERSE MOTIVES AND GRADED DERIVED CATEGORY
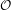 ${\mathcal{O}}$
${\mathcal{O}}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 26 February 2016, pp. 347-395
- Print publication:
- April 2018
-
- Article
- Export citation
REFINED MOTIVIC DIMENSION OF SOME FERMAT VARIETIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 25 November 2015, pp. 223-230
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
KUDLA’S MODULARITY CONJECTURE AND FORMAL FOURIER–JACOBI SERIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 01 October 2015, e7
-
- Article
-
- You have access
- Open access
- Export citation
Étale motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 24 September 2015, pp. 556-666
- Print publication:
- March 2016
-
- Article
- Export citation
PARTIALLY AMPLE LINE BUNDLES ON TORIC VARIETIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 587-598
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
Algebraic Cycles on Quadric Sections of Cubics in ℙ4 under the Action of Symplectomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 14 July 2015, pp. 377-392
-
- Article
- Export citation
Le complémentaire des puissances
 $n$-ièmes dans un corps de nombres est un ensemble diophantien
$n$-ièmes dans un corps de nombres est un ensemble diophantien
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 22 June 2015, pp. 1965-1980
- Print publication:
- October 2015
-
- Article
- Export citation
Hilbert series of residual intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 09 June 2015, pp. 1663-1687
- Print publication:
- September 2015
-
- Article
- Export citation
Purity for graded potentials and quantum cluster positivity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 19 May 2015, pp. 1913-1944
- Print publication:
- October 2015
-
- Article
- Export citation
Computing Néron–Severi groups and cycle class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 04 February 2015, pp. 713-734
- Print publication:
- April 2015
-
- Article
- Export citation
Mixed motivic sheaves (and weights for them) exist if ‘ordinary’ mixed motives do
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 917-956
- Print publication:
- May 2015
-
- Article
- Export citation
On a filtration of
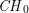 $\mathit{CH}_{0}$ for an abelian variety
$\mathit{CH}_{0}$ for an abelian variety
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 435-460
- Print publication:
- March 2015
-
- Article
- Export citation
ON DIFFERENCES BETWEEN THE BORDER RANK AND THE SMOOTHABLE RANK OF A POLYNOMIAL
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 401-413
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
DERIVED ALGEBRAIC COBORDISM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 30 October 2014, pp. 407-443
- Print publication:
- April 2016
-
- Article
- Export citation
Koszul Complexes and Pole Order Filtrations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 333-354
-
- Article
-
- You have access
- Export citation
La conjecture de Tate entière pour les cubiques de dimension quatre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 16 October 2014, pp. 253-264
- Print publication:
- February 2015
-
- Article
- Export citation
Hermitian forms over quaternion algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 15 September 2014, pp. 2073-2094
- Print publication:
- December 2014
-
- Article
- Export citation
Trihyperkähler reduction and instanton bundles on
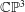 $\mathbb{C}\mathbb{P}^{3}$
$\mathbb{C}\mathbb{P}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1836-1868
- Print publication:
- November 2014
-
- Article
- Export citation
Examples of
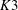 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 14-35
-
- Article
-
- You have access
- Export citation