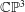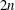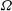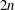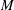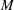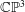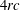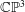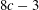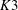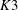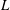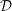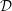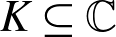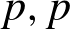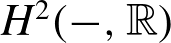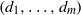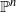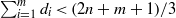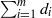Refine listing
Actions for selected content:
262 results in 14Cxx
La conjecture de Tate entière pour les cubiques de dimension quatre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 16 October 2014, pp. 253-264
- Print publication:
- February 2015
-
- Article
- Export citation
Hermitian forms over quaternion algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 15 September 2014, pp. 2073-2094
- Print publication:
- December 2014
-
- Article
- Export citation
Trihyperkähler reduction and instanton bundles on
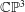 $\mathbb{C}\mathbb{P}^{3}$
$\mathbb{C}\mathbb{P}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1836-1868
- Print publication:
- November 2014
-
- Article
- Export citation
Examples of
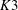 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 14-35
-
- Article
-
- You have access
- Export citation
CHOW GROUPS, CHOW COHOMOLOGY, AND LINEAR VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 24 June 2014, e17
-
- Article
-
- You have access
- Open access
- Export citation
Universal polynomials for singular curves on surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 06 June 2014, pp. 1169-1182
- Print publication:
- July 2014
-
- Article
- Export citation
Higher Chow cycles on Abelian surfaces and a non-Archimedean analogue of the Hodge-
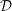 ${\mathcal{D}}$-conjecture
${\mathcal{D}}$-conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 691-711
- Print publication:
- April 2014
-
- Article
- Export citation
One-cycles on rationally connected varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 396-408
- Print publication:
- March 2014
-
- Article
- Export citation
MULTIPLICATIVE SUB-HODGE STRUCTURES OF CONJUGATE VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 18 February 2014, e1
-
- Article
-
- You have access
- Open access
- Export citation
A vanishing theorem and symbolic powers of planar point ideals
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 373-387
-
- Article
-
- You have access
- Export citation
ON THE INTEGRAL HODGE AND TATE CONJECTURES OVER A NUMBER FIELD
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 12 September 2013, e4
-
- Article
-
- You have access
- Open access
- Export citation
Smash nilpotent cycles on varieties dominated by products of curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 1511-1518
- Print publication:
- September 2013
-
- Article
- Export citation
The maximum likelihood degree of a very affine variety
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 24 May 2013, pp. 1245-1266
- Print publication:
- August 2013
-
- Article
- Export citation
GENERIC VANISHING THEORY VIA MIXED HODGE MODULES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 17 May 2013, e1
-
- Article
-
- You have access
- Open access
- Export citation
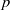 $p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES
$p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 17 May 2013, e1
-
- Article
-
- You have access
- Open access
- Export citation
Spaces of rational curves on complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 26 March 2013, pp. 1041-1060
- Print publication:
- June 2013
-
- Article
- Export citation
The Hodge ring of Kähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 637-657
- Print publication:
- April 2013
-
- Article
- Export citation
The standard conjectures for holomorphic symplectic varieties deformation equivalent to Hilbert schemes of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 481-494
- Print publication:
- March 2013
-
- Article
- Export citation
Hyperplane arrangements of Torelli type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 14 December 2012, pp. 309-332
- Print publication:
- February 2013
-
- Article
- Export citation
Zariski chambers on surfaces of high Picard number
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 219-230
-
- Article
-
- You have access
- Export citation