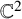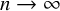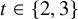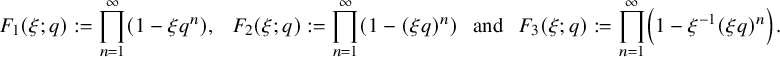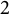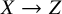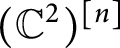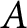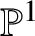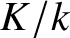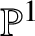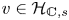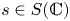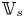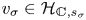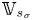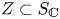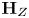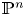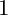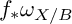Refine listing
Actions for selected content:
262 results in 14Cxx
Intersection theory of nef b-divisor classes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1563-1594
- Print publication:
- July 2022
-
- Article
- Export citation
Distributions on partitions arising from Hilbert schemes and hook lengths
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 29 June 2022, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion codimension
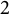 $2$ cycles on supersingular abelian varieties
$2$ cycles on supersingular abelian varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 458-466
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shokurov’s conjecture on conic bundles with canonical singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chow rings of stacks of prestable curves I
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 May 2022, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting Betti distributions of Hilbert schemes on n points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 May 2022, pp. 243-258
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unramified logarithmic Hodge–Witt cohomology and
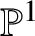 $\mathbb {P}^1$-invariance
$\mathbb {P}^1$-invariance
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 March 2022, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sur la lissité du schéma Quot ponctuel emboîté
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 178-184
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chow groups and L-derivatives of automorphic motives for unitary groups, II.
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute Hodge and ℓ-adic monodromy
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 568-584
- Print publication:
- March 2022
-
- Article
- Export citation
ZERO-CYCLES ON NORMAL PROJECTIVE VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 2241-2295
- Print publication:
- September 2023
-
- Article
- Export citation
The integral Hodge conjecture for two-dimensional Calabi–Yau categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 12 April 2022, pp. 287-333
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion properties of modified diagonal classes on triple products of modular curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 68-86
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GYSIN TRIANGLES IN THE CATEGORY OF MOTIFS WITH MODULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 06 January 2022, pp. 2131-2154
- Print publication:
- September 2023
-
- Article
- Export citation
Schiffer variations and the generic Torelli theorem for hypersurfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 89-122
- Print publication:
- January 2022
-
- Article
- Export citation
Tevelev degrees and Hurwitz moduli spaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 03 December 2021, pp. 479-510
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FUJITA DECOMPOSITION AND MASSEY PRODUCT FOR FIBERED VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 29 November 2021, pp. 624-652
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomological invariants of root stacks and admissible double coverings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 November 2021, pp. 202-224
- Print publication:
- February 2023
-
- Article
- Export citation
Free quotients of fundamental groups of smooth quasi-projective varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 27 October 2021, pp. 924-946
-
- Article
- Export citation