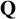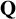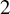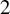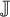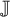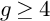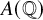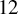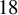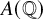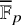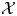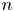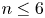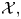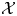Refine listing
Actions for selected content:
361 results in 14Gxx
“The six-functor formalism for rigid analytic motives” – Erratum
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 February 2025, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the linear AFL: the non-basic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 385-425
- Print publication:
- February 2025
-
- Article
- Export citation
Positivity, plethysm and hyperbolicity of Siegel varieties in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 257-304
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complete verification of strong BSD for many modular abelian surfaces over
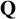 ${\mathbf {Q}}$
${\mathbf {Q}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rich representations and superrigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 2249-2272
- Print publication:
- August 2025
-
- Article
- Export citation
AN UPPER BOUND FOR THE GENERALISED GREATEST COMMON DIVISOR OF RATIONAL POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 248-253
- Print publication:
- October 2025
-
- Article
- Export citation
The Ekedahl–Oort stratification and the semi-module stratification
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The isotrivial case in the Mordell-Lang conjecture for semiabelian varieties defined over fields of positive characteristic
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 461-476
- Print publication:
- June 2025
-
- Article
- Export citation
Uniformity of quasi-integral points of bounded degree in higher-dimensional orbits
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 15-29
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of Shimura curves in
 $ \mathscr {A}_g$
$ \mathscr {A}_g$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion points and concurrent exceptional curves on del Pezzo surfaces of degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 634-652
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 93-103
- Print publication:
- March 2025
-
- Article
- Export citation
On the properness of the moduli space of stable surfaces over
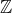 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ODA’S PROBLEM AND SPECIAL LOCI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 503-539
- Print publication:
- March 2025
-
- Article
- Export citation
Rational torsion points on abelian surfaces with quaternionic multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 November 2024, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mod p points on shimura varieties of parahoric level
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding geometrically integral del Pezzo surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 October 2024, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds on the height of K-semistable Fano varieties I, the toric case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 10 October 2024, pp. 2366-2406
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Low-degree Hurwitz stacks in the Grothendieck ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1784-1849
- Print publication:
- August 2024
-
- Article
- Export citation