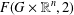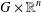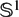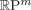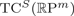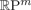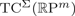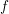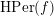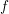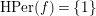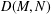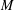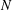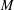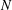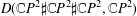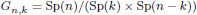Refine listing
Actions for selected content:
54 results in 55Mxx
Topological complexity of real Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 2013-2029
- Print publication:
- December 2021
-
- Article
- Export citation
The Brouwer invariance theorems in reverse mathematics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e51
-
- Article
-
- You have access
- Open access
- Export citation
Concentration of positive solutions for a class of fractional p-Kirchhoff type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 May 2020, pp. 601-651
- Print publication:
- April 2021
-
- Article
- Export citation
On Steenrod 𝕃-homology, generalized manifolds, and surgery
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 20 March 2020, pp. 579-607
-
- Article
- Export citation
Bisecting measures with hyperplane arrangements
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 31 October 2019, pp. 639-647
- Print publication:
- November 2020
-
- Article
- Export citation
Anosov diffeomorphisms of products I. Negative curvature and rational homology spheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 553-569
- Print publication:
- February 2021
-
- Article
- Export citation
Global fixed points for nilpotent actions on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3339-3367
- Print publication:
- December 2020
-
- Article
- Export citation
CATEGORY AND TOPOLOGICAL COMPLEXITY OF THE CONFIGURATION SPACE
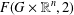 $F(G\times \mathbb{R}^{n},2)$
$F(G\times \mathbb{R}^{n},2)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 24 May 2019, pp. 507-517
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Grothendieck Ring of Varieties with Actions of Finite Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 08 March 2019, pp. 925-948
-
- Article
- Export citation
An n-dimensional Klein bottle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1207-1221
- Print publication:
- October 2019
-
- Article
- Export citation
FREE ACTIONS OF SOME COMPACT GROUPS ON MILNOR MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 727-742
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
LUSTERNIK–SCHNIRELMANN CATEGORY BASED ON THE DISCRETE CONLEY INDEX THEORY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 30 October 2018, pp. 693-704
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Symmetric Bi-Skew Maps and Symmetrized Motion Planning in Projective Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1087-1100
-
- Article
- Export citation
ANY CYCLIC QUADRILATERAL CAN BE INSCRIBED IN ANY CLOSED CONVEX SMOOTH CURVE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 31 May 2018, e7
-
- Article
-
- You have access
- Open access
- Export citation
FREE ACTION OF FINITE GROUPS ON SPACES OF COHOMOLOGY TYPE (0, b)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 673-680
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
HOMOTOPY MINIMAL PERIODS FOR HYPERBOLIC MAPS ON INFRA-NILMANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 1-18
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON INTEGERS OCCURRING AS THE MAPPING DEGREE BETWEEN QUASITORIC 4-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 289-312
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Morse Theory and the Lusternik–Schnirelmann Category of Quaternionic Grassmannians
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 441-449
-
- Article
- Export citation
Representing homotopy classes by maps with certain minimality root properties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1005-1015
- Print publication:
- October 2016
-
- Article
- Export citation
Equivariant Maps from Stiefel Bundles to Vector Bundles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 01 June 2016, pp. 231-250
-
- Article
- Export citation