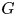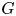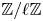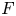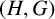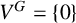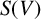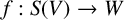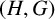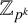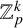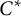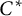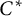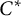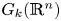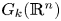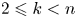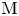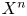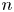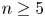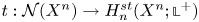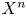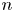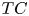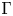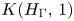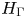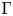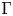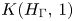Refine listing
Actions for selected content:
54 results in 55Mxx
Equivariant category and topological complexity of wedges
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-20
-
- Article
- Export citation
On properties of effective topological complexity and effective Lusternik–Schnirelmann category
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2025, pp. 1-36
-
- Article
- Export citation
Equivariant parametrized topological complexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-24
-
- Article
- Export citation
Equivariant covering type and the number of vertices in equivariant triangulations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-32
-
- Article
- Export citation
A study of the Ganea conjecture for topological complexity by using weak topological complexity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 21 October 2024, pp. 241-261
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic base change of cuspidal automorphic representations over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1959-2004
- Print publication:
- September 2024
-
- Article
- Export citation
Linked orbits of homeomorphisms of the plane and Gambaudo–Kolev Theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 103-108
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLE LOOSE MAPS BETWEEN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 554-563
- Print publication:
- December 2024
-
- Article
- Export citation
Various topological complexities of small covers and real Bott manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 December 2023, pp. 1061-1086
- Print publication:
- June 2025
-
- Article
- Export citation
Fixed point sets and the fundamental group II: Euler characteristics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 10 October 2023, pp. 1661-1680
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shape index, Brouwer degree and Poincaré–Hopf theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 September 2023, pp. 413-428
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on virtual duality and automorphism groups of right-angled Artin groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 573-581
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ESTIMATING THE SIZE OF THE
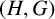 $(H, G)$-COINCIDENCES SET IN REPRESENTATION SPHERES
$(H, G)$-COINCIDENCES SET IN REPRESENTATION SPHERES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 313-319
- Print publication:
- April 2023
-
- Article
- Export citation
The generator rank of subhomogeneous
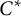 $C^*\!$-algebras
$C^*\!$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1314-1342
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum to “Topological complexity of real Grassmannians”
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 1071-1072
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
On the topological complexity and zero-divisor cup-length of real Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 31 March 2022, pp. 702-717
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The cohomology rings of real toric spaces and smooth real toric varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 720-737
- Print publication:
- June 2022
-
- Article
- Export citation
Generalized manifolds, normal invariants, and 𝕃-homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 574-589
-
- Article
- Export citation
Right-angled Artin groups, polyhedral products and the
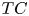 ${{\sf {TC}}}$-generating function
${{\sf {TC}}}$-generating function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 11 June 2021, pp. 649-673
- Print publication:
- June 2022
-
- Article
- Export citation
Homotopic distance between maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 22 February 2021, pp. 73-93
- Print publication:
- January 2022
-
- Article
- Export citation