Refine listing
Actions for selected content:
54 results in 55Mxx
AVERAGING FORMULA FOR NIELSEN NUMBERS OF MAPS ON INFRA-SOLVMANIFOLDS OF TYPE (R) – CORRIGENDUM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 207-212
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
COARSE AMENABILITY AND DISCRETENESS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 21 October 2015, pp. 65-77
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
The Laitinen Conjecture for finite non-solvable groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 303-336
-
- Article
-
- You have access
- Export citation
A twisted topological trace formula for Hecke operators and liftings from symplectic to general linear groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 65-120
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Topological complexity of collision-free motion planning on surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 649-660
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Cohomology rings of almost-direct products of free groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 465-479
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Betti numbers of fixed point sets and multiplicities of indecomposable summands
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-172
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Manifolds that fail to be co-dimension 2 fibrators necessarily cover themselves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-68
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
The torsion of the group of homeomorphisms of powers of the long line
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 311-322
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Lusternik-Schnirelmann category and Morse decompositions
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 299-305
- Print publication:
- December 2000
-
- Article
- Export citation
The Urysohn-Menger sum formula: an extension of the Dydak-Walsh theorem to dimension one
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-282
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
The least number of coincidence points on surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-38
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Inscribed squares and square-like quadrilaterals in closed curves
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 187-197
- Print publication:
- December 1989
-
- Article
- Export citation
The degree of the gradient of a coercive functional
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 413-415
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
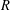
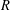
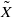 by gluing together 2
by gluing together 2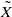 and get formulas for the traces of Hecke operators ℋ acting on the cohomology of
and get formulas for the traces of Hecke operators ℋ acting on the cohomology of 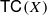 is a numerical homotopy invariant of a topological space
is a numerical homotopy invariant of a topological space 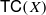 measures the complexity of motion planning algorithms which can be designed for the system. In this paper, we compute the topological complexity of the configuration space of
measures the complexity of motion planning algorithms which can be designed for the system. In this paper, we compute the topological complexity of the configuration space of 