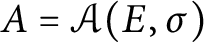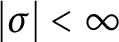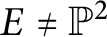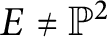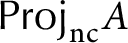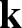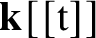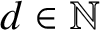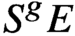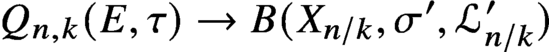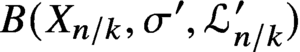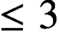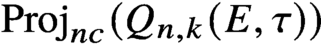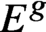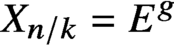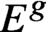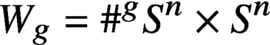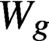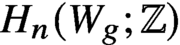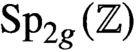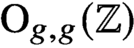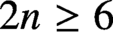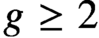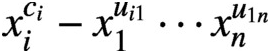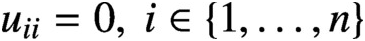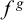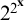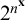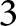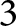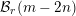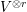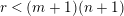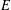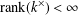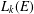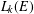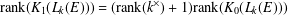Refine listing
Actions for selected content:
84 results in 16Wxx
Quantum projective planes finite over their centers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 53-67
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arquile Varieties – Varieties Consisting of Power Series in a Single Variable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 December 2021, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert’s 17th problem in free skew fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EVERY GRADED IDEAL OF A LEAVITT PATH ALGEBRA IS GRADED ISOMORPHIC TO A LEAVITT PATH ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 August 2021, pp. 248-256
- Print publication:
- April 2022
-
- Article
- Export citation
AS-REGULARITY OF GEOMETRIC ALGEBRAS OF PLANE CUBIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 22 June 2021, pp. 193-217
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
Two theorems on balanced braces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 262-278
-
- Article
- Export citation
The Plectic Weight Filtration on Cohomology of Shimura Varieties and Partial Frobenius
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 12 April 2021, e30
-
- Article
-
- You have access
- Open access
- Export citation
GRADED TWISTED CALABI–YAU ALGEBRAS ARE GENERALIZED ARTIN–SCHELTER REGULAR
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 100-153
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Formality conjecture for minimal surfaces of Kodaira dimension 0
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 February 2021, pp. 215-235
- Print publication:
- February 2021
-
- Article
- Export citation
Maps from Feigin and Odesskii's elliptic algebras to twisted homogeneous coordinate rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e4
-
- Article
-
- You have access
- Open access
- Export citation
The cohomology of Torelli groups is algebraic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 16 December 2020, e64
-
- Article
-
- You have access
- Open access
- Export citation
CRITICAL BINOMIAL IDEALS OF NORTHCOTT TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 48-70
- Print publication:
- February 2021
-
- Article
- Export citation
ASYMPTOTIC ANALYSIS OF SKOLEM’S EXPONENTIAL FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 04 September 2020, pp. 758-782
- Print publication:
- June 2022
-
- Article
- Export citation
2-LOCAL DERIVATIONS ON SEMISIMPLE BANACH ALGEBRAS WITH MINIMAL LEFT IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 July 2020, pp. 321-332
- Print publication:
- June 2021
-
- Article
- Export citation
A Complete Classification of 3-dimensional Quadratic AS-regular Algebras of Type EC
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 123-141
- Print publication:
- March 2021
-
- Article
- Export citation
THE FREE ENERGY OF THE TWO-DIMENSIONAL DILUTE BOSE GAS. I. LOWER BOUND
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 April 2020, e20
-
- Article
-
- You have access
- Open access
- Export citation
On a Lie Algebraic Approach to Abelian Extensions of Associative Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 26 March 2020, pp. 25-38
- Print publication:
- March 2021
-
- Article
- Export citation
ODD–EVEN DECOMPOSITION OF FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 104-108
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
THE SECOND FUNDAMENTAL THEOREM OF INVARIANT THEORY FOR THE ORTHOSYMPLECTIC SUPERGROUP
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 04 December 2019, pp. 52-76
- Print publication:
- June 2021
-
- Article
- Export citation
ALGEBRAIC CUNTZ–KRIEGER ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 23 September 2019, pp. 93-111
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation