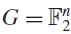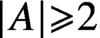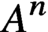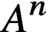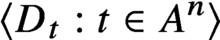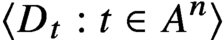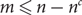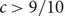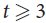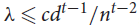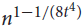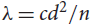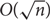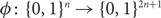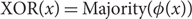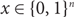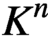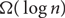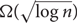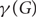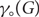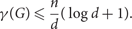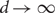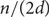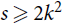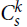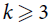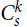Refine listing
Actions for selected content:
218 results in 05Dxx
Universal and unavoidable graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 15 April 2021, pp. 942-955
-
- Article
-
- You have access
- Open access
- Export citation
Ramsey-type numbers involving graphs and hypergraphs with large girth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 722-740
-
- Article
- Export citation
On the size-Ramsey number of grid graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 06 April 2021, pp. 670-685
-
- Article
- Export citation
On symmetric intersecting families of vectors
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 18 March 2021, pp. 899-904
-
- Article
- Export citation
A proof of a conjecture of Gyárfás, Lehel, Sárközy and Schelp on Berge-cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 654-669
-
- Article
- Export citation
RAMSEY’S COHEIRS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 377-391
- Print publication:
- March 2022
-
- Article
- Export citation
A variant of the Corners theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 02 February 2021, pp. 607-621
- Print publication:
- November 2021
-
- Article
- Export citation
A structure theorem for stochastic processes indexed by the discrete hypercube
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 January 2021, e8
-
- Article
-
- You have access
- Open access
- Export citation
A counterexample to the Bollobás–Riordan conjectures on sparse graph limits
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 27 January 2021, pp. 796-799
-
- Article
- Export citation
Full rainbow matchings in graphs and hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 762-780
-
- Article
- Export citation
Boxes, extended boxes and sets of positive upper density in the Euclidean space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 481-501
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
The length of an s-increasing sequence of r-tuples
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 686-721
-
- Article
- Export citation
Proof of a conjecture of Galvin
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 December 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation
Near-perfect clique-factors in sparse pseudorandom graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 11 December 2020, pp. 570-590
-
- Article
- Export citation
Lipschitz bijections between boolean functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 513-525
-
- Article
- Export citation
THE NUMBER OF ROOTS OF A POLYNOMIAL SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 369-378
- Print publication:
- June 2021
-
- Article
- Export citation
PSEUDO-FINITE SETS, PSEUDO-O-MINIMALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 577-599
- Print publication:
- June 2021
-
- Article
- Export citation
A simplified disproof of Beck’s three permutations conjecture and an application to root-mean-squared discrepancy
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 398-411
-
- Article
- Export citation
Independent dominating sets in graphs of girth five
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 15 October 2020, pp. 344-359
-
- Article
- Export citation
Covering and tiling hypergraphs with tight cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 13 October 2020, pp. 288-329
-
- Article
- Export citation