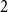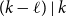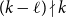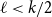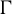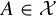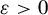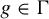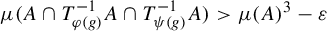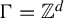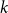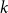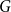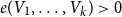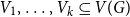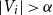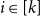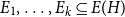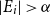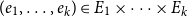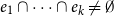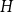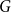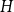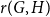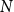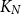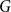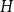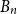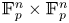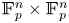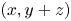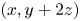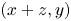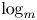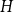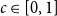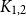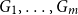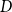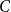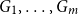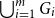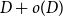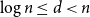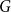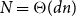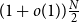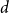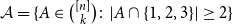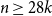Refine listing
Actions for selected content:
218 results in 05Dxx
The List-Ramsey threshold for families of graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 829-851
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Ramsey numbers of daisies I
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 795-806
-
- Article
- Export citation
On the Ramsey numbers of daisies II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 742-768
-
- Article
- Export citation
Counting spanning subgraphs in dense hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 30 May 2024, pp. 729-741
-
- Article
- Export citation
A generalisation of Varnavides’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 724-728
-
- Article
- Export citation
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Khintchine-type double recurrence in abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 April 2024, pp. 1-33
- Print publication:
- January 2025
-
- Article
- Export citation
A NEW PERSPECTIVE ON SEMI-RETRACTIONS AND THE RAMSEY PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 945-979
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON JUDICIOUS BISECTIONS OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 401-408
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Large monochromatic components in expansive hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 467-483
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A class of graphs of zero Turán density in a hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 404-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a conjecture of Conlon, Fox, and Wigderson
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 432-445
-
- Article
- Export citation
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation
POLISH SPACE PARTITION PRINCIPLES AND THE HALPERN–LÄUCHLI THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1798-1816
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARTITION OF LARGE SUBSETS OF SEMIGROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-6
-
- Article
- Export citation
Subsets of
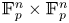 $\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 176-236
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Threshold graphs maximise homomorphism densities
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 300-318
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A special case of Vu’s conjecture: colouring nearly disjoint graphs of bounded maximum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 179-195
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spanning subdivisions in Dirac graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 121-128
-
- Article
- Export citation
Intersecting families without unique shadow
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 91-109
-
- Article
- Export citation