Refine listing
Actions for selected content:
218 results in 05Dxx
A Stability Result for the Union-Closed Size Problem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 18 August 2015, pp. 399-418
-
- Article
- Export citation
An Improvement of the Beck–Fiala Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 06 July 2015, pp. 380-398
-
- Article
- Export citation
A NOTE ON RAMSEY NUMBERS FOR FANS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 13 May 2015, pp. 19-23
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
DYADIC SHIFT RANDOMIZATION IN CLASSICAL DISCREPANCY THEORY
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 06 May 2015, pp. 183-209
- Print publication:
- 2016
-
- Article
- Export citation
Forcing a sparse minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 16 April 2015, pp. 300-322
-
- Article
- Export citation
On the Chromatic Thresholds of Hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 06 March 2015, pp. 172-212
-
- Article
- Export citation
The (7, 4)-Conjecture in Finite Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 10 February 2015, pp. 680-686
-
- Article
- Export citation
Partial Shadows of Set Systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 5 / September 2015
- Published online by Cambridge University Press:
- 20 January 2015, pp. 825-828
-
- Article
- Export citation
Combinatorial Structures on van der Waerden sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 929-953
-
- Article
- Export citation
The Sharp Threshold for Maximum-Size Sum-Free Subsets in Even-Order Abelian Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 609-640
-
- Article
- Export citation
PRIMITIVE RECURSIVE BOUNDS FOR THE FINITE VERSION OF GOWERS’
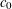 $c_{0}$ THEOREM
$c_{0}$ THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 501-522
- Print publication:
- September 2015
-
- Article
- Export citation
ON CONFIGURATIONS WHERE THE LOOMIS–WHITNEY INEQUALITY IS NEARLY SHARP AND APPLICATIONS TO THE FURSTENBERG SET PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 145-161
- Print publication:
- January 2015
-
- Article
- Export citation
A Short Proof of the Random Ramsey Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 22 December 2014, pp. 130-144
-
- Article
- Export citation
Minimum Number of Monotone Subsequences of Length 4 in Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 19 December 2014, pp. 658-679
-
- Article
- Export citation
A NOTE ON ORDER-TYPE HOMOGENEOUS POINT SETS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 19 December 2013, pp. 37-42
- Print publication:
- January 2014
-
- Article
- Export citation
ALMOST ALL SETS OF
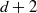 $d+ 2$ POINTS ON THE
$d+ 2$ POINTS ON THE 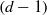 $(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE
$(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 28 March 2013, pp. 267-268
- Print publication:
- July 2013
-
- Article
- Export citation
SUMSETS AND DIFFERENCE SETS CONTAINING A COMMON TERM OF A SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 26 September 2011, pp. 79-83
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
Central sets in commutative semigroups and partition regularity of systems of linear equations
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 169-186
- Print publication:
- December 1993
-
- Article
- Export citation
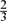
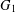
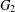
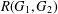
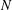
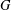
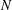
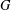
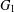
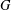
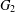
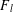
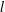
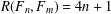
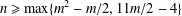
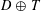
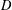
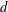
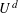
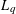
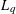
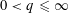
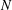
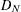
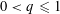
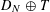
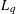
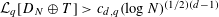
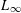
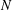
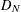
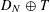
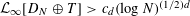
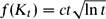
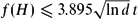
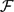
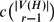
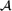

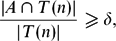
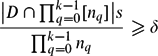
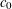
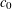
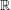
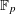
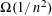
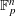
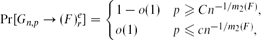
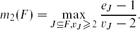
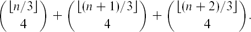
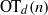
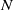
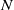
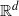

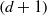
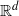
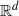
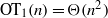
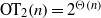
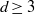
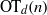
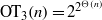
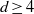
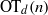
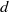
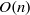
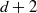
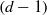
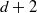
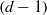
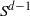
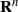
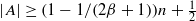 , then (
, then (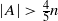 , then (
, then ( cannot be improved.
cannot be improved.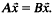 . In particular, the system of equations
. In particular, the system of equations 