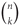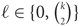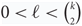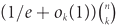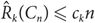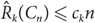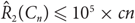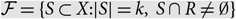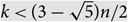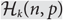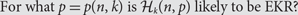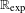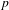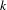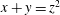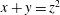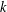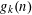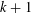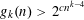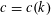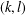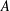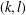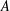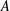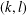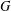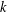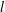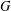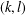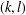Refine listing
Actions for selected content:
218 results in 05Dxx
Edge-statistics on large graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. 163-189
-
- Article
- Export citation
The Induced Removal Lemma in Sparse Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 30 September 2019, pp. 153-162
-
- Article
- Export citation
On the Size-Ramsey Number of Cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 17 July 2019, pp. 871-880
-
- Article
- Export citation
Triforce and corners
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 209-223
- Print publication:
- July 2020
-
- Article
- Export citation
A natural barrier in random greedy hypergraph matching
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 27 June 2019, pp. 816-825
-
- Article
- Export citation
On the union of intersecting families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 27 June 2019, pp. 826-839
-
- Article
- Export citation
On Erdős–Ko–Rado for random hypergraphs I
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 881-916
-
- Article
- Export citation
A fast new algorithm for weak graph regularity
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 777-790
-
- Article
- Export citation
RAMSEY GROWTH IN SOME NIP STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 February 2019, pp. 1-29
- Print publication:
- January 2021
-
- Article
- Export citation
MONOID ACTIONS AND ULTRAFILTER METHODS IN RAMSEY THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 29 January 2019, e2
-
- Article
-
- You have access
- Open access
- Export citation
Monochromatic Solutions to
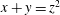 $x+y=z^{2}$
$x+y=z^{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 579-605
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
THE ERDŐS–SZEKERES PROBLEM AND AN INDUCED RAMSEY QUESTION
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 702-707
- Print publication:
- 2019
-
- Article
- Export citation
LONELY RUNNERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 677-701
- Print publication:
- 2019
-
- Article
- Export citation
THE MAXIMUM SIZE OF
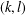 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A Combinatorial Approach to Small Ball Inequalities for Sums and Differences
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 November 2018, pp. 100-129
-
- Article
- Export citation
On Erdős–Ko–Rado for Random Hypergraphs II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 18 October 2018, pp. 61-80
-
- Article
- Export citation
An Extremal Graph Problem with a Transcendental Solution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 26 June 2018, pp. 303-324
-
- Article
- Export citation
Bounding the Size of an Almost-Equidistant Set in Euclidean Space
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 13 June 2018, pp. 280-286
-
- Article
- Export citation
Fast Property Testing and Metrics for Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 24 May 2018, pp. 539-579
-
- Article
- Export citation
A (5,5)-Colouring of Kn with Few Colours
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 09 May 2018, pp. 892-912
-
- Article
- Export citation