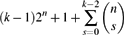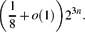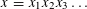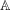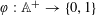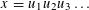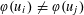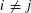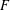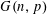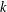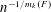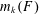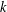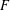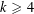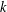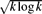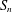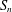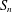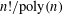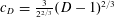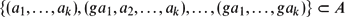Refine listing
Actions for selected content:
218 results in 05Dxx
Triangle-Tilings in Graphs Without Large Independent Sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 09 May 2018, pp. 449-474
-
- Article
- Export citation
Multicolour Sunflowers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 974-987
-
- Article
- Export citation
A Stability Theorem for Matchings in Tripartite 3-Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 5 / September 2018
- Published online by Cambridge University Press:
- 02 April 2018, pp. 774-793
-
- Article
- Export citation
On Quantitative Noise Stability and Influences for Discrete andContinuous Models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 23 March 2018, pp. 334-357
-
- Article
- Export citation
MONOCHROMATIC FACTORIZATIONS OF WORDS AND PERIODICITY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 115-123
- Print publication:
- 2018
-
- Article
- Export citation
The Minimum Number of Edges in Uniform Hypergraphs with Property O
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 19 December 2017, pp. 531-538
-
- Article
- Export citation
Robust Tverberg and Colourful Carathéodory Results via Random Choice
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 19 December 2017, pp. 427-440
-
- Article
- Export citation
SYMMETRIC AND ASYMMETRIC RAMSEY PROPERTIES IN RANDOM HYPERGRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 November 2017, e28
-
- Article
-
- You have access
- Open access
- Export citation
Counting Intersecting and Pairs of Cross-Intersecting Families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 60-68
-
- Article
- Export citation
Colourings of Uniform Hypergraphs with Large Girth and Applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 245-273
-
- Article
- Export citation
LOW-DEGREE BOOLEAN FUNCTIONS ON
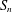 $S_{n}$ , WITH AN APPLICATION TO ISOPERIMETRY
$S_{n}$ , WITH AN APPLICATION TO ISOPERIMETRY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 03 October 2017, e23
-
- Article
-
- You have access
- Open access
- Export citation
On a random search tree: asymptotic enumeration of vertices by distance from leaves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 850-876
- Print publication:
- September 2017
-
- Article
- Export citation
Computing absorbing times via fluid approximations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 768-790
- Print publication:
- September 2017
-
- Article
- Export citation
Induced Subgraphs With Many Distinct Degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 01 August 2017, pp. 110-123
-
- Article
- Export citation
UPPER BOUNDS FOR SUNFLOWER-FREE SETS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 June 2017, e15
-
- Article
-
- You have access
- Open access
- Export citation
Corners Over Quasirandom Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 6 / November 2017
- Published online by Cambridge University Press:
- 06 June 2017, pp. 944-951
-
- Article
- Export citation
Convex Polygons in Geometric Triangulations†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 30 May 2017, pp. 641-659
-
- Article
- Export citation
The Proofs of Two Directed Paths Conjectures of Bollobás and Leader
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 22 May 2017, pp. 762-774
-
- Article
- Export citation
An Inequality for Functions on the Hamming Cube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 468-480
-
- Article
- Export citation
Erdős–Ko–Rado for Random Hypergraphs: Asymptotics and Stability
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 406-422
-
- Article
- Export citation