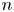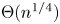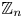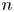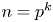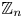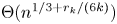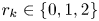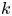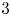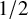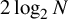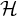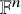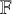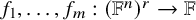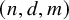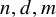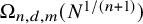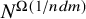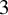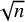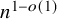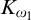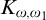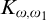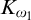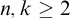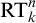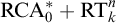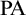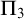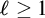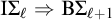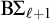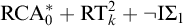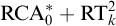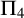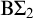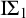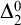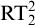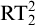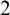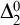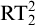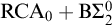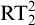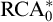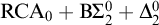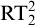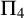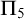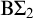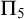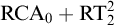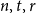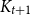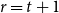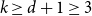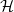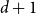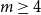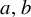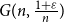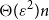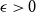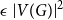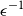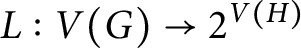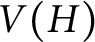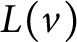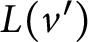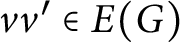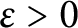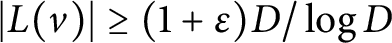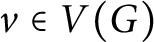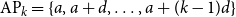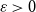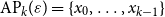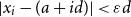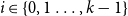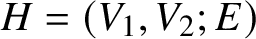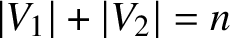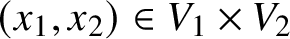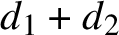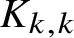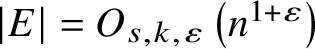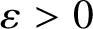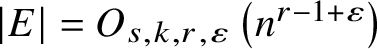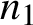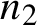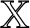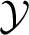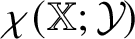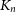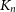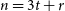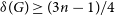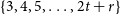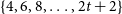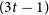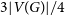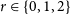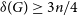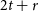Refine listing
Actions for selected content:
218 results in 05Dxx
Discrepancy in modular arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 2082-2108
- Print publication:
- November 2022
-
- Article
- Export citation
Ramsey properties of algebraic graphs and hypergraphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 24 October 2022, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cycles of many lengths in Hamiltonian graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 31 August 2022, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAKER–BREAKER GAMES ON
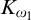 $ K_{\omega _1}$ AND
$ K_{\omega _1}$ AND 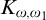 $K_{\omega ,\omega _1}$
$K_{\omega ,\omega _1}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 697-703
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOW STRONG IS RAMSEY’S THEOREM IF INFINITY CAN BE WEAK?
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 14 June 2022, pp. 620-639
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complete subgraphs in a multipartite graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1092-1101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hypergraphs without non-trivial intersecting subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1076-1091
-
- Article
- Export citation
Joint ergodicity of fractional powers of primes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Short proofs for long induced paths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 870-878
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Removal lemmas and approximate homomorphisms
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 721-736
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Independent transversals in bipartite correspondence-covers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 882-894
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A blurred view of Van der Waerden type theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 26 November 2021, pp. 684-701
-
- Article
- Export citation
STRUCTURAL CONSIDERATIONS OF RAMSEY ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1677-1692
- Print publication:
- December 2022
-
- Article
- Export citation
Zarankiewicz’s problem for semilinear hypergraphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 31 August 2021, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
All finite sets are Ramsey in the maximum norm
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 August 2021, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Combinatorial anti-concentration inequalities, with applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 30 June 2021, pp. 227-248
- Print publication:
- September 2021
-
- Article
- Export citation
Some remarks on the Zarankiewicz problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 155-161
- Print publication:
- July 2022
-
- Article
- Export citation
Monochromatic paths and cycles in 2-edge-coloured graphs with large minimum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 14 June 2021, pp. 109-122
-
- Article
- Export citation
Density theorems for anisotropic point configurations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 1244-1276
- Print publication:
- October 2022
-
- Article
- Export citation
Turán theorems for unavoidable patterns
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 423-442
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation