Refine listing
Actions for selected content:
56 results in 39Axx
ON PERIODIC SOLUTIONS FOR FIRST-ORDER DIFFERENTIAL EQUATIONS INVOLVING THE DISTRIBUTIONAL HENSTOCK–KURZWEIL INTEGRAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 06 February 2012, pp. 327-338
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
CHARACTERIZING DIGITAL STRAIGHTNESS AND DIGITAL CONVEXITY BY MEANS OF DIFFERENCE OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. 355-380
- Print publication:
- July 2011
-
- Article
- Export citation
GLOBAL ASYMPTOTIC STABILITY FOR GENERAL SYMMETRIC RATIONAL DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 02 October 2009, pp. 251-259
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
τ-function of discrete isomonodromy transformations and probability
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 747-772
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Hitting Time and Inverse Problems for Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 640-649
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
MULTIPLE SOLUTIONS OF PERIODIC BOUNDARY VALUE PROBLEMS FOR FIRST-ORDER DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 1-11
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
REMARKS ON ℓ1 AND
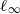 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 345-365
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Hypertranscendance des systèmes aux différences diagonaux
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 565-581
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
A classification scheme for nonoscilatory solutions of a higher order neutral nonlinear difference equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 122-142
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
The Frobenius–Harper technique in a general recurrence model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 30-47
- Print publication:
- March 1999
-
- Article
- Export citation
Difference equations in abstract spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 277-284
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Lp–Lrestimates for the Poisson semigroup on homogeneous trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 20-32
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Generalized theorem of Hartman-Grobman on measure chains
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-191
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
Linear independence of translations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-133
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
Chaotic difference equations in Rn
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-225
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
Algebraic independence by a method of Mahler
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 2 / March 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-188
- Print publication:
- March 1979
-
- Article
-
- You have access
- Export citation
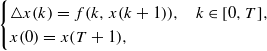
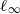 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
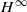 -calculus, and give a complete characterization of this condition in the case of Banach spaces which are
-calculus, and give a complete characterization of this condition in the case of Banach spaces which are 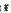 be a homogeneous tree of degree at least three. In this paper we investigate for which values of
be a homogeneous tree of degree at least three. In this paper we investigate for which values of