Refine listing
Actions for selected content:
171 results in 53Dxx
The Calabi–Yau equation on the Kodaira–Thurston manifold
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 24 September 2010, pp. 437-447
- Print publication:
- April 2011
-
- Article
- Export citation
HOMOGENEOUS AND H-CONTACT UNIT TANGENT SPHERE BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 12 May 2010, pp. 323-337
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Complex submanifolds, connections and asymptotics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 373-383
-
- Article
-
- You have access
- Export citation
The diffeotopy group of S1×S2 via contact topology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 18 March 2010, pp. 1096-1112
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Rigid subsets of symplectic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 773-826
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Spectral numbers in Floer theories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1581-1592
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
The Bochner-flat cone of a CR manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 747-773
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
On the local structure of Dirac manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 774-786
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Quantum cohomology of the Grassmannian and alternate Thom–Sebastiani
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 221-246
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
Maximal symplectic packings in
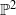
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1558-1575
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
A generalisation of the Morse inequalities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-386
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
 is a Riemannian
is a Riemannian 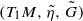 is
is