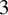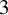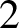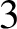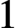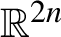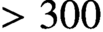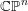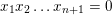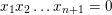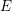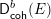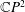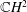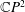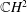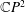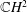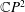Refine listing
Actions for selected content:
171 results in 53Dxx
Equidistribution of horospheres in non-positive curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 28 October 2021, pp. 460-479
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reeb orbits that force topological entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 3025-3068
- Print publication:
- October 2022
-
- Article
- Export citation
Quasimaps to GIT fibre bundles and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 August 2021, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost existence from the feral perspective and some questions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 792-834
- Print publication:
- February 2022
-
- Article
- Export citation
Every symplectic manifold is a (linear) coadjoint orbit
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 345-360
- Print publication:
- June 2022
-
- Article
- Export citation
ERRATUM/CORRIGENDUM, OCTOBER 2020, FOR ’A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION’ (J. INST. MATH. JUSSIEU 19 (2018), 1509–1519)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 16 April 2021, pp. 275-277
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
Pseudorotations of the
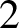 $2$-disc and Reeb flows on the
$2$-disc and Reeb flows on the 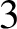 $3$-sphere
$3$-sphere
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 402-436
- Print publication:
- February 2022
-
- Article
- Export citation
Fukaya categories of surfaces, spherical objects and mapping class groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 18 March 2021, e26
-
- Article
-
- You have access
- Open access
- Export citation
Deformation of Dirac operators along orbits and quantization of noncompact Hamiltonian torus manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 March 2021, pp. 1062-1092
- Print publication:
- August 2022
-
- Article
- Export citation
A HYDRODYNAMICAL HOMOTOPY CO-MOMENTUM MAP AND A MULTISYMPLECTIC INTERPRETATION OF HIGHER-ORDER LINKING NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 335-354
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
Equivariant wrapped Floer homology and symmetric periodic Reeb orbits
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 February 2021, pp. 1708-1763
- Print publication:
- May 2022
-
- Article
- Export citation
The symplectic geometry of higher Auslander algebras: Symmetric products of disks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 February 2021, e10
-
- Article
-
- You have access
- Open access
- Export citation
SFT COMPUTATIONS AND INTERSECTION THEORY IN HIGHER-DIMENSIONAL CONTACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1219-1270
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Tropically constructed Lagrangians in mirror quintic threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e58
-
- Article
-
- You have access
- Open access
- Export citation
Lagrangian foliations and Anosov symplectomorphisms on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3325-3335
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
Homology supported in Lagrangian submanifolds in mirror quintic threefolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 709-724
- Print publication:
- September 2021
-
- Article
- Export citation
POINCARÉ AND SOBOLEV INEQUALITIES FOR DIFFERENTIAL FORMS IN HEISENBERG GROUPS AND CONTACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 29 June 2020, pp. 869-920
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Homological mirror symmetry for higher-dimensional pairs of pants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 1310-1347
- Print publication:
- July 2020
-
- Article
- Export citation
Computing a categorical Gromov–Witten invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 1275-1309
- Print publication:
- July 2020
-
- Article
- Export citation
Generalized
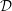 ${\mathcal{D}}$-Einstein Real Hypersurfaces in
${\mathcal{D}}$-Einstein Real Hypersurfaces in 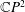 $\mathbb{C}P^{2}$ and
$\mathbb{C}P^{2}$ and 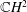 $\mathbb{C}H^{2}$
$\mathbb{C}H^{2}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 27 February 2020, pp. 909-920
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation