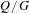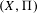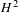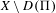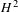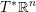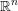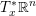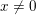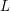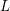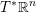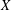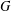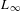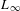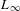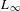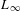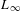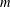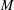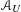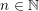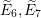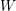Refine listing
Actions for selected content:
171 results in 53Dxx
On geodesic flows with symmetries and closed magnetic geodesics on orbifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1480-1509
- Print publication:
- June 2020
-
- Article
- Export citation
A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 09 November 2018, pp. 1509-1519
- Print publication:
- September 2020
-
- Article
- Export citation
Systolic ratio, index of closed orbits and convexity for tight contact forms on the three-sphere
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2643-2680
- Print publication:
- December 2018
-
- Article
- Export citation
Dehn twist exact sequences through Lagrangian cobordism
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 05 November 2018, pp. 2485-2533
- Print publication:
- December 2018
-
- Article
- Export citation
CONTACT METRIC THREE-MANIFOLDS WITH CONSTANT SCALAR TORSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 234-255
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
THE HALL ALGEBRAS OF SURFACES I
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 22 October 2018, pp. 971-1028
- Print publication:
- May 2020
-
- Article
- Export citation
Geodesic Flows Modelled by Expansive Flows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 61-95
-
- Article
- Export citation
Nearby Lagrangian fibers and Whitney sphere links
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 685-718
- Print publication:
- April 2018
-
- Article
- Export citation
AN EQUIVARIANT DESCRIPTION OF CERTAIN HOLOMORPHIC SYMPLECTIC VARIETIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 207-214
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
LIE ALGEBROIDS AS
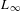 $L_{\infty }$ SPACES
$L_{\infty }$ SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 13 February 2018, pp. 487-535
- Print publication:
- March 2020
-
- Article
- Export citation
POTENTIALS OF A FROBENIUS-LIKE STRUCTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 681-693
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL GERSTENHABER–BATALIN–VILKOVISKY ALGEBRAS FOR CALABI–YAU HYPERSURFACE COMPLEMENTS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 07 June 2018, pp. 637-651
- Print publication:
- 2018
-
- Article
- Export citation
Rigid constellations of closed Reeb orbits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 04 September 2017, pp. 2394-2444
- Print publication:
- November 2017
-
- Article
- Export citation
Holomorphic Legendrian curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 29 June 2017, pp. 1945-1986
- Print publication:
- September 2017
-
- Article
- Export citation
DUBROVIN’S SUPERPOTENTIAL AS A GLOBAL SPECTRAL CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 17 April 2017, pp. 449-497
- Print publication:
- May 2019
-
- Article
- Export citation
Elliptic singularities on log symplectic manifolds and Feigin–Odesskii Poisson brackets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 717-744
- Print publication:
- April 2017
-
- Article
- Export citation
Towards a symplectic version of the Chevalley restriction theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 647-666
- Print publication:
- March 2017
-
- Article
- Export citation
On the contact mapping class group ofLegendrian circle bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 01 February 2017, pp. 294-312
- Print publication:
- February 2017
-
- Article
- Export citation
On quasi-classical limits of DQ-algebroids
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 41-67
- Print publication:
- January 2017
-
- Article
- Export citation
CONFORMALLY FLAT CONTACT THREE-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 03 November 2016, pp. 177-189
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation