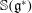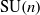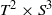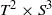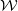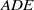Refine listing
Actions for selected content:
171 results in 53Dxx
Products of twists, geodesic lengths and Thurston shears
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 313-350
- Print publication:
- February 2015
-
- Article
- Export citation
Bounding Lagrangian widths via geodesic paths
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 17 September 2014, pp. 2143-2183
- Print publication:
- December 2014
-
- Article
- Export citation
Reduction of Homogeneous Riemannian Structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 18 July 2014, pp. 81-106
-
- Article
-
- You have access
- Export citation
Minimal genus and fibering of canonical surfaces via disk decomposition
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 77-108
-
- Article
-
- You have access
- Export citation
Deformations of the Lie–Poisson sphere of a compact semisimple Lie algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 27 March 2014, pp. 568-578
- Print publication:
- April 2014
-
- Article
- Export citation
Implosion for hyperkähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 1592-1630
- Print publication:
- September 2013
-
- Article
- Export citation
Extremal Sasakian geometry on
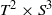 ${T}^{2} \times {S}^{3} $ and related manifolds
${T}^{2} \times {S}^{3} $ and related manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1431-1456
- Print publication:
- August 2013
-
- Article
- Export citation
Ellipsoid embeddings and symplectic packing stability
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 04 March 2013, pp. 889-902
- Print publication:
- May 2013
-
- Article
- Export citation
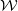 $\mathcal {W}$-constraints for the total descendant potential of a simple singularity
$\mathcal {W}$-constraints for the total descendant potential of a simple singularity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 840-888
- Print publication:
- May 2013
-
- Article
- Export citation
Singular polynomials from orbit spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 15 October 2012, pp. 1867-1879
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
A symplectic proof of a theorem of Franks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 1969-1984
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Symplectic T7, T8 singularities and Lagrangian tangency orders
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 28 August 2012, pp. 657-683
-
- Article
-
- You have access
- Export citation
A note about invariant SKT structures and generalized Kähler structures on flag manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 21 March 2012, pp. 543-549
-
- Article
-
- You have access
- Export citation
Contact homology of good toric contact manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 304-334
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
A REMARK ON THE BRYLINSKI CONJECTURE FOR ORBIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 11 October 2011, pp. 1-12
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Springer theory via the Hitchin fibration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 1635-1670
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
SYMPLECTIC STRUCTURES ON STATISTICAL MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 15 June 2011, pp. 371-384
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
GEOMETRIC PHASES IN THE QUANTISATION OF BOSONS AND FERMIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 29 June 2011, pp. 221-235
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
PARAMETRIZED STRICT DEFORMATION QUANTIZATION OF C*-BUNDLES AND HILBERT C*-MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 18 May 2011, pp. 25-38
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Notes on contact Ricci solitons
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 47-53
-
- Article
-
- You have access
- Export citation
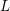
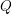
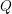
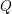
 . The situation when
. The situation when