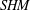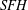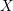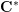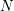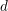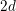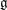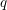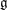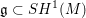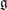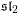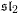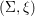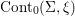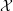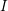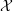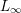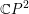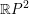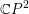Refine listing
Actions for selected content:
171 results in 53Dxx
SYMPLECTIC FILLINGS OF LINKS OF QUOTIENT SURFACE SINGULARITIES – CORRIGENDUM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 225 / March 2017
- Published online by Cambridge University Press:
- 24 October 2016, pp. 207-212
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
SUPERORBITS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1065-1120
- Print publication:
- November 2018
-
- Article
- Export citation
MULTISYMPLECTIC VARIATIONAL INTEGRATORS FOR NONSMOOTH LAGRANGIAN CONTINUUM MECHANICS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 08 July 2016, e19
-
- Article
-
- You have access
- Open access
- Export citation
Non-contractible periodic orbits in Hamiltonian dynamics on closed symplectic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 17 June 2016, pp. 1777-1799
- Print publication:
- September 2016
-
- Article
- Export citation
Adjoint Orbits of Semi-Simple Lie Groups and Lagrangian Submanifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 361-385
-
- Article
- Export citation
A CONTACT INVARIANT IN SUTURED MONOPOLE HOMOLOGY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 10 June 2016, e12
-
- Article
-
- You have access
- Open access
- Export citation
BEREZIN–TOEPLITZ QUANTIZATION, HYPERKÄHLER MANIFOLDS, AND MULTISYMPLECTIC MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 167-187
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
A finiteness theorem on symplectic singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1225-1236
- Print publication:
- June 2016
-
- Article
- Export citation
Floer cohomology of
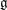 $\mathfrak{g}$-equivariant Lagrangian branes
$\mathfrak{g}$-equivariant Lagrangian branes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 1071-1110
- Print publication:
- May 2016
-
- Article
- Export citation
Orderability and the Weinstein conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 24 September 2015, pp. 2251-2272
- Print publication:
- December 2015
-
- Article
- Export citation
REAL HYPERSURFACES OF NON-FLAT COMPLEX SPACE FORMS WITH GENERALIZED ξ-PARALLEL JACOBI STRUCTURE OPERATOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 23 July 2015, pp. 677-687
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF A GLOBAL NEIGHBOURHOOD
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 717-726
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
Pseudoholomorphic tori in the Kodaira–Thurston manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 16 July 2015, pp. 2212-2250
- Print publication:
- December 2015
-
- Article
- Export citation
A mirror theorem for toric stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1878-1912
- Print publication:
- October 2015
-
- Article
-
- You have access
- Open access
- Export citation
Quantum reconstruction for Fano bundles on projective space
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-28
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Simultaneous deformations and Poisson geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 1763-1790
- Print publication:
- September 2015
-
- Article
- Export citation
On an exotic Lagrangian torus in
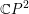 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 27 February 2015, pp. 1372-1394
- Print publication:
- July 2015
-
- Article
- Export citation
ON BI-HARMONIC HYPERSURFACES IN EUCLIDEAN SPACE OF ARBITRARY DIMENSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 633-642
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
SINGULAR COTANGENT MODEL
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 415-430
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF RICCI FLAT METRICS AND LAGRANGIAN SUBMANIFOLDS IN TERMS OF THE VARIATIONAL PROBLEM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 643-651
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation