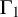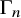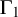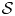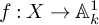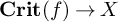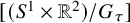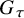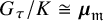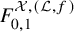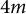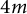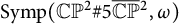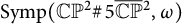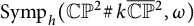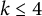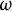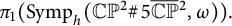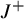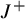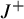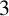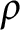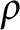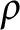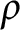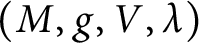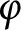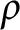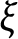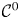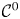Refine listing
Actions for selected content:
171 results in 53Dxx
Classification of generalized Einstein metrics on three-dimensional Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 2038-2095
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant Brill–Noether theory for elliptic operators and superrigidity of J-holomorphic maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hofer–Zehnder conjecture on weighted projective spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 87-108
- Print publication:
- January 2023
-
- Article
- Export citation
Quantitative Heegaard Floer cohomology and the Calabi invariant
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 December 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pseudo-holomorphic dynamics in the restricted three-body problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 663-693
- Print publication:
- May 2023
-
- Article
- Export citation
On Anosovity, divergence and bi-contact surgery
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 3288-3310
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Euler continuants in noncommutative quasi-Poisson geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coisotropic Ekeland–Hofer capacities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1564-1608
- Print publication:
- October 2023
-
- Article
- Export citation
Symplectic reduction along a submanifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 18 October 2022, pp. 1878-1934
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A DERIVED LAGRANGIAN FIBRATION ON THE DERIVED CRITICAL LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 August 2022, pp. 311-345
- Print publication:
- January 2024
-
- Article
- Export citation
Open-closed Gromov-Witten invariants of 3-dimensional Calabi-Yau smooth toric DM stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 July 2022, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on Lagrangian submanifolds in symplectic
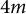 $4m$-manifolds
$4m$-manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 525-531
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Loops in the fundamental group of
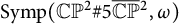 ${\mbox{Symp}} ({\mathbb C}{\mathbb P}^2\# \mbox{5}\overline { \mathbb C\mathbb P}\,\!^2,\omega )$ which are not represented by circle actions
${\mbox{Symp}} ({\mathbb C}{\mathbb P}^2\# \mbox{5}\overline { \mathbb C\mathbb P}\,\!^2,\omega )$ which are not represented by circle actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 1226-1271
- Print publication:
- August 2023
-
- Article
- Export citation
SOLUTIONS OF THE tt*-TODA EQUATIONS AND QUANTUM COHOMOLOGY OF MINUSCULE FLAG MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 990-1004
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
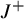 $J^+$-invariants for planar two-center Stark–Zeeman systems
$J^+$-invariants for planar two-center Stark–Zeeman systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 2258-2292
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTACT SURGERY GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 146-157
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fibrations in semitoric and generalized complex geometry
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 March 2022, pp. 645-685
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACTIONS OF MONOIDAL CATEGORIES AND REPRESENTATIONS OF CARTAN TYPE LIE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 2367-2402
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some characterizations of
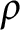 $\rho $-Einstein solitons on Sasakian manifolds
$\rho $-Einstein solitons on Sasakian manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 1036-1049
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
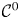 $\mathbb {\mathcal {C}}^{0}$-rigidity of Lagrangian submanifolds and punctured holomorphic disks in the cotangent bundle
$\mathbb {\mathcal {C}}^{0}$-rigidity of Lagrangian submanifolds and punctured holomorphic disks in the cotangent bundle
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 03 November 2021, pp. 2433-2493
- Print publication:
- November 2021
-
- Article
- Export citation