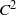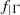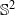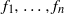Refine listing
Actions for selected content:
145 results in 37Exx
ON SUMMABILITY CONDITIONS FOR INTERVAL MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 308-315
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Boundaries of instability zones for symplectic twist maps
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 08 February 2013, pp. 19-41
- Print publication:
- January 2014
-
- Article
- Export citation
Des points fixes communs pour des difféomorphismes de
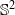 ${ \mathbb{S} }^{2} $ qui commutent et préservent une mesure de probabilité
${ \mathbb{S} }^{2} $ qui commutent et préservent une mesure de probabilité
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 08 February 2013, pp. 821-851
- Print publication:
- October 2013
-
- Article
- Export citation
ON SHRINKING TARGETS FOR ℤm ACTIONS ON TORI
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 16 April 2010, pp. 193-202
- Print publication:
- July 2010
-
- Article
- Export citation
AN ALMOST EVERYWHERE VERSION OF SMÍTAL’S ORDER–CHAOS DICHOTOMY FOR INTERVAL MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 29-50
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation