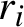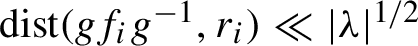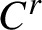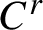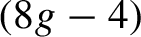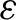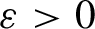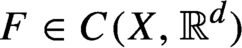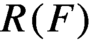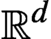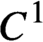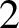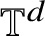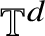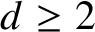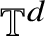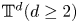Refine listing
Actions for selected content:
145 results in 37Exx
Lyapunov exponent of random dynamical systems on the circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 2080-2107
- Print publication:
- June 2022
-
- Article
- Export citation
Inverse problems and rigidity questions in billiard dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 1023-1056
- Print publication:
- March 2022
-
- Article
- Export citation
Dynamic aspects of tumour–immune system interaction under a periodic immunotherapy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 606-645
-
- Article
- Export citation
Thermodynamics of smooth models of pseudo–Anosov homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 1284-1326
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation
A characterization of a map whose inverse limit is an arc
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2533-2549
- Print publication:
- August 2022
-
- Article
- Export citation
Homoclinic orbits for area preserving diffeomorphisms of surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 1122-1165
- Print publication:
- March 2022
-
- Article
- Export citation
Flexibility of measure-theoretic entropy of boundary maps associated to Fuchsian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 14 April 2021, pp. 389-401
- Print publication:
- February 2022
-
- Article
- Export citation
The bifurcation locus for numbers of bounded type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2239-2269
- Print publication:
- July 2022
-
- Article
- Export citation
Generic chaos on dendrites
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 2108-2150
- Print publication:
- June 2022
-
- Article
- Export citation
Non-existence of sublinear diffusion for a class of torus homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 1517-1547
- Print publication:
- April 2022
-
- Article
- Export citation
Generic rotation sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 250-262
- Print publication:
- January 2022
-
- Article
- Export citation
Invariant densities for random systems of the interval
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 141-179
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Hausdorff measure and Assouad dimension of generic self-conformal IFS on the line
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2051-2081
- Print publication:
- December 2021
-
- Article
- Export citation
Kneading sequences for toy models of Hénon maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 3521-3540
- Print publication:
- December 2021
-
- Article
- Export citation
Periodic point free homeomorphisms and irrational rotation factors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 2946-2982
- Print publication:
- October 2021
-
- Article
- Export citation
Foliations and conjugacy, II: the Mendes conjecture for time-one maps of flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3307-3324
- Print publication:
- November 2021
-
- Article
- Export citation
On the rotation sets of generic homeomorphisms on the torus
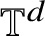 ${\mathbb T^d}$
${\mathbb T^d}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 07 October 2020, pp. 2983-3022
- Print publication:
- October 2021
-
- Article
- Export citation
Loewner evolution of hedgehogs and 2-conformal measures of circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2734-2753
- Print publication:
- September 2021
-
- Article
- Export citation
Continuous flows generate few homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 25 August 2020, pp. 971-983
-
- Article
- Export citation
STOCHASTIC POTENTIALS OF INTERMITTENT MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 18 June 2020, pp. 145-153
- Print publication:
- February 2021
-
- Article
- Export citation