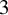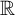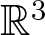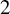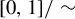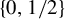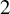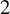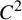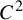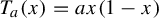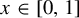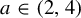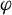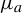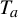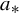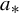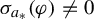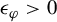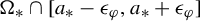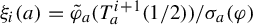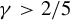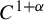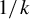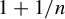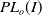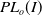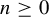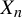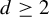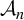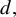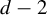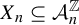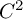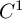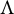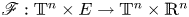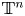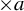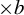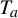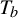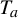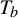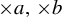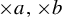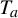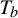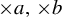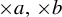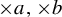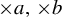Refine listing
Actions for selected content:
145 results in 37Exx
New classes of quasigeodesic Anosov flows in
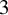 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2095-2131
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A criterion to detect a non-trivial homology of an invariant set of a flow in
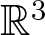 $\mathbb{R}^3$
$\mathbb{R}^3$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irrational rotations and
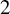 $2$-filling rays
$2$-filling rays
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1673-1697
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite data rigidity for one-dimensional expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1597-1618
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Volume and Euler classes in bounded cohomology of transformation groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 02 October 2024, pp. 34-49
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Birkhoff attractors of dissipative billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 989-1047
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A parameter ASIP for the quadratic family
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 663-703
- Print publication:
- March 2025
-
- Article
- Export citation
On the critical regularity of nilpotent groups acting on the interval: the metabelian case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1177-1198
- Print publication:
- April 2025
-
- Article
- Export citation
Multifractal analysis of homological growth rates for hyperbolic surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 849-883
- Print publication:
- March 2025
-
- Article
- Export citation
Linked orbits of homeomorphisms of the plane and Gambaudo–Kolev Theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 103-108
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Girth Alternative for subgroups of
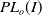 $PL_o(I)$
$PL_o(I)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-10
- Print publication:
- January 2025
-
- Article
- Export citation
Isochronous centers and flat Finsler metrics (I)
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1294-1314
- Print publication:
- August 2025
-
- Article
- Export citation
On the Hausdorff dimension of invariant measures of piecewise smooth circle homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 3599-3629
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure transfer and S-adic developments for subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 3120-3154
- Print publication:
- November 2024
-
- Article
- Export citation
Systems involving mean value formulas on trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 January 2024, pp. 351-383
- Print publication:
- April 2025
-
- Article
- Export citation
ON RESIDUES AND CONJUGACIES FOR GERMS OF 1-D PARABOLIC DIFFEOMORPHISMS IN FINITE REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1821-1855
- Print publication:
- July 2024
-
- Article
- Export citation
Effective rigidity away from the boundary for centrally symmetric billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 1741-1756
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Piecewise contracting maps on the interval: Hausdorff dimension, entropy, and attractors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 318-327
- Print publication:
- June 2024
-
- Article
- Export citation
Moser's theorem with frequency-preserving
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 29 August 2023, pp. 1473-1503
- Print publication:
- October 2024
-
- Article
- Export citation
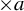 $\times a$ and
$\times a$ and 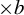 $\times b$ empirical measures, the irregular set and entropy
$\times b$ empirical measures, the irregular set and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1673-1692
- Print publication:
- June 2024
-
- Article
- Export citation