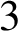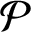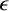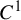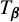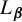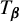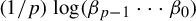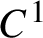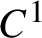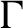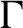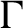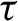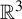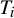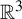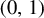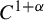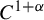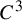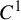Refine listing
Actions for selected content:
145 results in 37Exx
RETRACTED - THE KRONECKER–WEYL EQUIDISTRIBUTION THEOREM AND GEODESICS IN 3-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2022, pp. 1-44
-
- Article
- Export citation
LI–YORKE CHAOS ALMOST EVERYWHERE: ON THE PERVASIVENESS OF DISJOINT EXTREMALLY SCRAMBLED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 132-143
- Print publication:
- August 2022
-
- Article
- Export citation
Distribution in the unit tangent bundle of the geodesics of given type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 24 January 2022, pp. 887-903
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Actions of symplectic homeomorphisms/diffeomorphisms on foliations by curves in dimension 2
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 20 January 2022, pp. 794-826
- Print publication:
- March 2023
-
- Article
- Export citation
Dynamical behavior of alternate base expansions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 22 December 2021, pp. 827-860
- Print publication:
- March 2023
-
- Article
- Export citation
Large deviation principle for piecewise monotonic maps with density of periodic measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 14 December 2021, pp. 861-872
- Print publication:
- March 2023
-
- Article
- Export citation
Non-differentiable irrational curves for
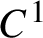 $C^1$ twist map
$C^1$ twist map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 491-499
- Print publication:
- February 2022
-
- Article
- Export citation
From curves to currents
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 November 2021, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures for interval maps without Lyapunov exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 663-691
- Print publication:
- February 2023
-
- Article
- Export citation
S-limit shadowing is generic for continuous Lebesgue measure-preserving circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 25 October 2021, pp. 78-98
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted cohomological equations for translation flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 22 October 2021, pp. 881-916
- Print publication:
- March 2022
-
- Article
- Export citation
Non-uniform ergodic properties of Hamiltonian flows with impacts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 20 October 2021, pp. 190-252
- Print publication:
- January 2023
-
- Article
- Export citation
The geometric index and attractors of homeomorphisms of
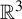 $\mathbb {R}^3$
$\mathbb {R}^3$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 50-77
- Print publication:
- January 2023
-
- Article
- Export citation
AN APERIODIC TILE WITH EDGE-TO-EDGE ORIENTATIONAL MATCHING RULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1727-1755
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homotopy Hubbard trees for post-singularly finite exponential maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 01 October 2021, pp. 253-298
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasisymmetric orbit-flexibility of multicritical circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3271-3310
- Print publication:
- November 2022
-
- Article
- Export citation
Examples of distorted interval diffeomorphisms of intermediate regularity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3311-3324
- Print publication:
- November 2022
-
- Article
- Export citation
Hyperbolicity of renormalization for dissipative gap mappings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 03 September 2021, pp. 3069-3110
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A non-Borel special alpha-limit set in the square
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 22 July 2021, pp. 2550-2560
- Print publication:
- August 2022
-
- Article
- Export citation
Markovian random iterations of homeomorphisms of the circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 2935-2956
- Print publication:
- September 2022
-
- Article
- Export citation