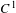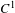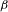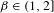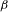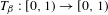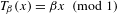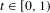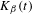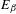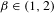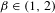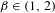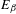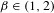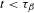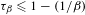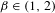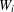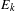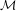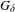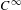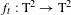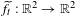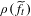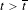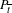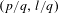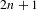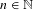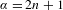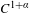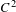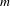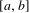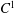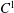Refine listing
Actions for selected content:
145 results in 37Exx
Lyapunov optimization for non-generic one-dimensional expanding Markov maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2571-2592
- Print publication:
- September 2020
-
- Article
- Export citation
The
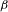 $\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
$\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2482-2514
- Print publication:
- September 2020
-
- Article
-
- You have access
- Open access
- Export citation
SYMMETRIC ITINERARY SETS: ALGORITHMS AND NONLINEAR EXAMPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 109-118
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Rates in almost sure invariance principle for slowly mixing dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 2317-2348
- Print publication:
- September 2020
-
- Article
- Export citation
Deviations in the Franks–Misiurewicz conjecture
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 2533-2540
- Print publication:
- September 2020
-
- Article
- Export citation
WEIERSTRASS PRYM EIGENFORMS IN GENUS FOUR
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 14 February 2019, pp. 2045-2085
- Print publication:
- November 2020
-
- Article
- Export citation
Cascades in the dynamics of affine interval exchange transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 2073-2097
- Print publication:
- August 2020
-
- Article
- Export citation
Dynamics and eigenvalues in dimension zero
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 04 January 2019, pp. 2434-2452
- Print publication:
- September 2020
-
- Article
- Export citation
Return- and hitting-time distributions of small sets in infinite measure preserving systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 02 January 2019, pp. 2239-2273
- Print publication:
- August 2020
-
- Article
- Export citation
ON TYPICALITY OF TRANSLATION FLOWS WHICH ARE DISJOINT WITH THEIR INVERSE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 11 December 2018, pp. 1677-1737
- Print publication:
- September 2020
-
- Article
- Export citation
A consequence of the growth of rotation sets for families of diffeomorphisms of the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1441-1458
- Print publication:
- June 2020
-
- Article
- Export citation
Embeddings of interval exchange transformations into planar piecewise isometries
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 23 October 2018, pp. 1153-1179
- Print publication:
- May 2020
-
- Article
- Export citation
Renormalization in the golden-mean semi-Siegel Hénon family: universality and non-rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 25 September 2018, pp. 1108-1152
- Print publication:
- April 2020
-
- Article
- Export citation
Rigidity, universality, and hyperbolicity of renormalization for critical circle maps with non-integer exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 25 September 2018, pp. 1282-1334
- Print publication:
- May 2020
-
- Article
- Export citation
Escaping orbits are rare in the quasi-periodic Fermi–Ulam ping-pong
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 06 September 2018, pp. 975-991
- Print publication:
- April 2020
-
- Article
- Export citation
Coagulation and universal scaling limits for critical Galton–Watson processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 504-542
- Print publication:
- June 2018
-
- Article
- Export citation
AN ELEMENTARY PROOF OF A THEOREM BY MATSUMOTO
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 05 October 2016, pp. 77-85
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
CENTRAL LIMIT THEOREM FOR THE MODULUS OF CONTINUITY OF AVERAGES OF OBSERVABLES ON TRANSVERSAL FAMILIES OF PIECEWISE EXPANDING UNIMODAL MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 13 July 2016, pp. 673-733
- Print publication:
- June 2018
-
- Article
- Export citation
ON ANNULAR MAPS OF THE TORUS AND SUBLINEAR DIFFUSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 4 / September 2018
- Published online by Cambridge University Press:
- 23 June 2016, pp. 913-978
- Print publication:
- September 2018
-
- Article
- Export citation
Sur les rapprochements par conjugaison en dimension 1 et classe
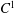 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 19 June 2014, pp. 1183-1195
- Print publication:
- July 2014
-
- Article
- Export citation