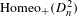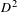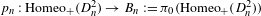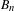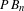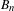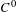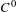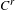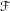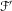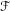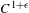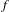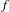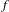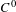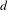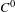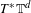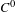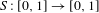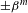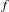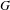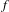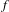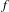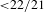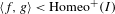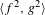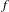Refine listing
Actions for selected content:
145 results in 37Exx
Non-realizability of the pure braid group as area-preserving homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 1988-1999
- Print publication:
- July 2021
-
- Article
- Export citation
Approximating integrals with respect to stationary probability measures of iterated function systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 2294-2310
- Print publication:
- August 2021
-
- Article
- Export citation
Big mapping class groups and rigidity of the simple circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 03 June 2020, pp. 1961-1987
- Print publication:
- July 2021
-
- Article
- Export citation
A spectral decomposition of the attractor of piecewise-contracting maps of the interval
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 05 May 2020, pp. 1940-1960
- Print publication:
- July 2021
-
- Article
- Export citation
Asymptotic escape rates and limiting distributions for multimodal maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 1656-1705
- Print publication:
- June 2021
-
- Article
- Export citation
A solution to Flinn’s conjecture on weakly expansive flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 1390-1396
- Print publication:
- May 2021
-
- Article
- Export citation
Entropy of general diffeomorphisms on line
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 18 February 2020, pp. 1139-1155
- Print publication:
- April 2021
-
- Article
- Export citation
Sobolev regularity of solutions of the cohomological equation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 685-789
- Print publication:
- March 2021
-
- Article
- Export citation
There are no proper topological hyperbolic homoclinic classes for area-preserving maps
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 12 November 2019, pp. 217-228
-
- Article
- Export citation
Endperiodic automorphisms of surfaces and foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 66-212
- Print publication:
- January 2021
-
- Article
- Export citation
A condition that implies full homotopical complexity of orbits for surface homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 24 September 2019, pp. 1-47
- Print publication:
- January 2021
-
- Article
- Export citation
A switched server system semiconjugate to a minimal interval exchange
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 682-708
-
- Article
- Export citation
The
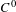 $C^{0}$ integrability of symplectic twist maps without conjugate points
$C^{0}$ integrability of symplectic twist maps without conjugate points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 August 2019, pp. 48-65
- Print publication:
- January 2021
-
- Article
- Export citation
ELASTIC GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e24
-
- Article
-
- You have access
- Open access
- Export citation
Quasi-Sturmian colorings on regular trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3403-3419
- Print publication:
- December 2020
-
- Article
- Export citation
Global fixed points for nilpotent actions on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3339-3367
- Print publication:
- December 2020
-
- Article
- Export citation
Generic point equivalence and Pisot numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3169-3180
- Print publication:
- December 2020
-
- Article
- Export citation
Constant slope, entropy, and horseshoes for a map on a tame graph
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 22 April 2019, pp. 2970-2994
- Print publication:
- November 2020
-
- Article
- Export citation
STABLE SETS OF CERTAIN NON-UNIFORMLY HYPERBOLIC HORSESHOES HAVE THE EXPECTED DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 04 April 2019, pp. 305-329
- Print publication:
- January 2021
-
- Article
- Export citation
2-chains and square roots of Thompson’s group
 $F$
$F$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2515-2532
- Print publication:
- September 2020
-
- Article
- Export citation