Refine listing
Actions for selected content:
424 results in 46Lxx
Twisted crossed products by coactions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 320-344
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Equivariant KK-theory for inverse limits of G-C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-211
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Crossed products of C*-algebras by *-endomorphisms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 204-212
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
On certain pairs of automorphisms of rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-38
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
The Toeplitz operator proof of noncommutative Bott periodicity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-251
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Full C*-Crossed product duality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 34-52
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
The symmetric algebra of quotients of an ultraprime Banach algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 75-87
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
A comment on certain p–shift algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-58
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Continuous-trace algebras from the bundle theoretic point of view
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 368-381
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
The structure of crossed products by smooth actions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 226-235
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
Fourier inversion formula for discrete nilpotent groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-422
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
On certain pairs of automorphisms of C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 197-211
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
Cartan subalgebras of regular extensions of von Neumann algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-274
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
Support of the joint spectral measure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 74-80
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Smooth derivations on abelian C*-dynamical systems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 247-264
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Representations of minimally almost periodic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-375
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Perturbations of type I Aw*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 407-413
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
Cp-classes of operators in C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-160
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Continuous trace C*-algebras with given Dixmer-Douady class
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 3 / June 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 394-407
- Print publication:
- June 1985
-
- Article
-
- You have access
- Export citation
Homogeneous C*-algebras whose spectra are tori
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-39
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
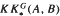 are extended to the setting of inverse limits of
are extended to the setting of inverse limits of 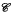 of ℳ. we show that ℳ ⋊
of ℳ. we show that ℳ ⋊ 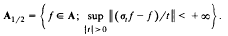
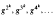 for some positive integer
for some positive integer 