Refine listing
Actions for selected content:
423 results in 46Lxx
THE PARTIAL-ISOMETRIC CROSSED PRODUCTS BY SEMIGROUPS OF ENDOMORPHISMS AS FULL CORNERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 145-166
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
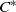 ${C}^{\ast } $-ALGEBRAS ASSOCIATED WITH LAMBDA-SYNCHRONIZING SUBSHIFTS AND FLOW EQUIVALENCE
${C}^{\ast } $-ALGEBRAS ASSOCIATED WITH LAMBDA-SYNCHRONIZING SUBSHIFTS AND FLOW EQUIVALENCE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 241-265
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
THE SIMILARITY DEGREE OF SOME
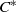 ${C}^{\ast } $-ALGEBRAS
${C}^{\ast } $-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 27 June 2013, pp. 60-69
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
FELL BUNDLES AND IMPRIMITIVITY THEOREMS: MANSFIELD’S AND FELL’S THEOREMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 68-75
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
OBSTRUCTIONS TO A GENERAL CHARACTERIZATION OF GRAPH CORRESPONDENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 169-188
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Remarks on some fundamental results about higher-rank graphs and their C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 April 2013, pp. 575-597
-
- Article
-
- You have access
- Export citation
THE ÉTALE GROUPOID OF AN INVERSE SEMIGROUP AS A GROUPOID OF FILTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 15 May 2013, pp. 234-256
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
On derivations and elementary operators on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 515-534
-
- Article
-
- You have access
- Export citation
GROUPOID
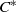 ${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 232-242
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
THE DUAL STRUCTURE OF CROSSED PRODUCT
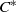 ${C}^{\ast } $-ALGEBRAS WITH FINITE GROUPS
${C}^{\ast } $-ALGEBRAS WITH FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 243-249
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Hochschild homology of Hopf algebras and free Yetter–Drinfeld resolutions of the counit
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 17 December 2012, pp. 658-678
- Print publication:
- April 2013
-
- Article
- Export citation
A higher category approach to twisted actions on c* -algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 387-426
-
- Article
-
- You have access
- Export citation
EVERY TOPOLOGICALLY AMENABLE LOCALLY COMPACT QUANTUM GROUP IS AMENABLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2012, pp. 149-151
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
A crossed-product approach to the Cuntz–Li algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 429-459
-
- Article
-
- You have access
- Export citation
On the AF-algebra of a Hecke eigenform
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 207-213
-
- Article
-
- You have access
- Export citation
ON TENSOR PRODUCTS OF WEAK MIXING VECTOR SEQUENCES AND THEIR APPLICATIONS TO UNIQUELY E-WEAK MIXING C*-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 04 October 2011, pp. 46-59
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
IDEALS IN OPERATOR SPACE PROJECTIVE TENSOR PRODUCT OF C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 18 November 2011, pp. 275-288
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
ORDER EMBEDDING OF A MATRIX ORDERED SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 21 June 2011, pp. 10-18
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Corrigendum: C*-envelopes of tensor algebras for multivariable dynamics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 20 May 2011, pp. 643-644
-
- Article
-
- You have access
- Export citation
STATES ON THE CUNTZ ALGEBRAS AND p-ADIC RANDOM WALKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 197-211
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
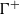
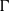
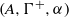
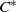
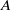

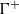
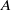
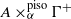
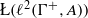

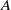
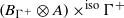
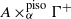
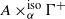
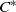
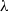
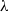
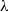
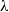
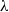
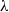
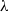
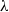
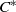
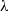
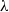
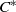
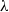
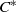
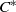
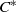
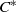
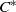

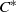
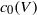
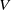
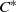
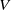
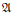 over the maximal ideal space of the centre of
over the maximal ideal space of the centre of 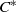
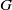
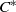
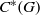
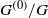
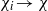
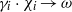
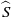
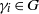
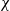
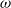
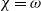
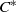
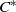
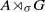
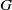
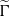
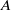
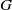
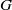
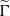
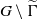
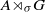
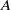
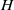
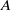
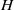
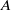
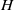
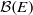
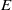
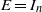
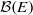
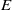
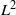
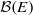
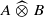 . As an application, a characterization of the prime ideals in the Banach *-algebra
. As an application, a characterization of the prime ideals in the Banach *-algebra 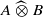 is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of
is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of 