Refine listing
Actions for selected content:
423 results in 46Lxx
EXTENSION ALGEBRAS OF CUNTZ ALGEBRA, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 83-90
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
COVERINGS OF SKEW-PRODUCTS AND CROSSED PRODUCTS BY COACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 379-398
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Hochschild cohomology of II1 factors with Cartan maximal abelian subalgebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 287-295
-
- Article
-
- You have access
- Export citation
CONTINUOUS AND DISCRETE FLOWS ON OPERATOR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 169-176
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
A KADISON–SAKAI-TYPE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 249-257
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Amalgamated free products of C*-bundles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 23-36
-
- Article
-
- You have access
- Export citation
Hecke C*-algebras and semi-direct products
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 127-153
-
- Article
-
- You have access
- Export citation
Morita equivalences and KK-theory for Banach algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 15 December 2008, pp. 565-593
- Print publication:
- July 2009
-
- Article
- Export citation
A MEAN ERGODIC THEOREM FOR ACTIONS OF AMENABLE QUANTUM GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 87-95
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
AMENABILITY FOR REAL C*-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 509-514
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
LOCAL PROPERTIES OF THE HOCHSCHILD COHOMOLOGY OF C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 117-130
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
THE K-THEORY OF SOME HIGHER RANK EXEL–LACA ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 21-38
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
A Class of Limit Algebras Associated with Directed Graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-368
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
C*-algebras associated with presentations of subshifts ii. ideal structure and lambda-graph subsystems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-385
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Operator algebras with a reduction property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-315
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Partial automorphisms of stable C*-algebras and Hilbert C*-bimodules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-398
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Real rank of C*-algebras associated with graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-147
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
One-sided ideals and approximate identities in operator algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-448
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
The Dixmier-Douady class of groupoid crossed products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-234
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Embeddings of ℓp into Non-commutative Spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-350
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
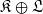 and
and 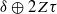 , where
, where 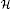 when
when 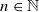 , bounded local
, bounded local 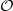 be a higher rank Exel–Laca algebra generated by an alphabet
be a higher rank Exel–Laca algebra generated by an alphabet 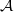 . If
. If 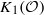 is trivial and
is trivial and  is isomorphic to
is isomorphic to 