Refine listing
Actions for selected content:
424 results in 46Lxx
Embeddings of ℓp into Non-commutative Spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-350
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Characteristic invatiant of tensor product actions and actions on crossed products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-376
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Categorical constructions in C*-algebra theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 97-114
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Discrete series of fusion algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-426
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Some irreducible free group representations in which a linear combination of the generators has an eigenvalue
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-286
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
On graph C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-160
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
On the Toeplitz algebras of right-angled and finite-type Artin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-246
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Elements of rings with equal spectral idempotents
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 137-152
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Three bimodules for Mansfield's imprimitivity theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-420
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
On the convergence of a sequence of completely positive maps to the identity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 340-348
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
C*-actions of r-discrete groupoids and inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-167
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation
Extremally rich C*-crossed products and the cancellation property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 285-301
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Crossed products of Hilbert C*-bimodules by bundles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-135
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
C*-crossed products by partial actions and actions of inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 32-46
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Representations of triangular subalgebras of groupoid C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-321
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
Hilbert C*-modules and conditional expectations on crossed products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 106-118
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Endomorphisms of type II1-factors and Cuntz algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-354
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
Discrete C*-coactions and C*-algebraic bundles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 204-221
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
Discrete coactions on C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 118-127
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Full coactions on Hilbert C*-modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 409-420
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
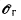 is canonically isomorphic to Cuntz-Krieger algebra corresponding to the adjacency matrix of γ. It is shown that if a countably infinite graph γ is strongly connected,
is canonically isomorphic to Cuntz-Krieger algebra corresponding to the adjacency matrix of γ. It is shown that if a countably infinite graph γ is strongly connected, 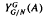 ; the bimodule assembled by Ng from Green's
; the bimodule assembled by Ng from Green's 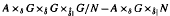 imprimitivity bimodule
imprimitivity bimodule 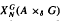 and Katayama duality; and the bimodule assembled from
and Katayama duality; and the bimodule assembled from 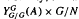 . We show that all three of these are isomorphic, so that the corresponding inducing maps on representations are identical. This can be interpreted as saying that Mansfield and Green induction are inverses of one another ‘modulo Katayama duality’. These results pass to twisted coactions; dual results starting with an action are also given.
. We show that all three of these are isomorphic, so that the corresponding inducing maps on representations are identical. This can be interpreted as saying that Mansfield and Green induction are inverses of one another ‘modulo Katayama duality’. These results pass to twisted coactions; dual results starting with an action are also given.