Refine listing
Actions for selected content:
424 results in 46Lxx
STATES ON THE CUNTZ ALGEBRAS AND p-ADIC RANDOM WALKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 197-211
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
C*-pseudo-multiplicative unitaries, Hopf C*-bimodules and their Fourier algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 04 February 2011, pp. 189-220
- Print publication:
- January 2012
-
- Article
- Export citation
SOME C*-ALGEBRAS ASSOCIATED TO QUANTUM GAUGE THEORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 18 May 2011, pp. 9-24
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
THE GELFAND SPECTRUM OF A NONCOMMUTATIVE C*-ALGEBRA: A TOPOS-THEORETIC APPROACH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 08 April 2011, pp. 39-52
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
FROM C*-ALGEBRA EXTENSIONS TO COMPACT QUANTUM METRIC SPACES, QUANTUM SU(2), PODLEŚ SPHERES AND OTHER EXAMPLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 09 June 2011, pp. 1-8
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
PARAMETRIZED STRICT DEFORMATION QUANTIZATION OF C*-BUNDLES AND HILBERT C*-MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 18 May 2011, pp. 25-38
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
AUTOMORPHISMS OF THE UHF ALGEBRA THAT DO NOT EXTEND TO THE CUNTZ ALGEBRA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 07 February 2011, pp. 309-315
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
TYPE DECOMPOSITION OF A PSEUDOEFFECT ALGEBRA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 28 February 2011, pp. 335-358
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Elementary operators and subhomogeneous C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 99-111
-
- Article
-
- You have access
- Export citation
LINEAR ORTHOGONALITY PRESERVERS OF HILBERT BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 05 November 2010, pp. 245-254
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Characterizing Jordan maps on C*-algebras through zero products
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 543-555
-
- Article
-
- You have access
- Export citation
More localized automorphisms of the Cuntz algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 619-631
-
- Article
-
- You have access
- Export citation
CO-REPRESENTATIONS OF HOPF–VON NEUMANN ALGEBRAS ON OPERATOR SPACES OTHER THAN COLUMN HILBERT SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 205-210
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Poisson boundary of the discrete quantum group
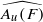
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 1073-1095
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
A CHARACTERIZATION OF SATURATED C*-ALGEBRAIC BUNDLES OVER FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 04 June 2010, pp. 363-383
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
C*-envelopes of tensor algebras for multivariable dynamics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 333-351
-
- Article
-
- You have access
- Export citation
PERIODIC 2-GRAPHS ARISING FROM SUBSHIFTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 23 March 2010, pp. 120-138
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Structural results for free Araki–Woods factors and their continuous cores
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 18 February 2010, pp. 741-767
- Print publication:
- October 2010
-
- Article
- Export citation
Uniform approximation by elementary operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 731-749
-
- Article
-
- You have access
- Export citation
On completely singular von Neumann subalgebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 607-618
-
- Article
-
- You have access
- Export citation
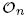 corresponding to permutation matrices in
corresponding to permutation matrices in 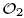 using labelled rooted trees. We also discuss those proper endomorphisms of these Cuntz algebras which restrict to automorphisms of their respective diagonals. In the case of
using labelled rooted trees. We also discuss those proper endomorphisms of these Cuntz algebras which restrict to automorphisms of their respective diagonals. In the case of 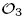 we compute the number of automorphisms of the diagonal induced by permutation matrices in
we compute the number of automorphisms of the diagonal induced by permutation matrices in 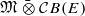 is a Banach algebra if and only if 𝔐 is subhomogeneous or
is a Banach algebra if and only if 𝔐 is subhomogeneous or 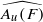
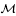 =
= 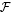 (
( and let
and let 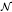 be a von Neumann subalgebra of ℳ. If
be a von Neumann subalgebra of ℳ. If 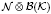 is singular in
is singular in 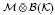 for every Hilbert space
for every Hilbert space 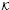 ,
, 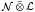 is completely singular in
is completely singular in 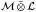 for every separable von Neumann algebra
for every separable von Neumann algebra 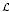 . As the second application, we prove that if
. As the second application, we prove that if 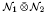 is completely singular in
is completely singular in 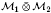 .
.