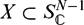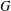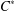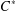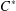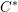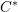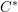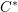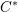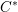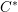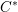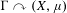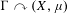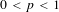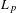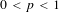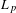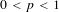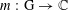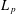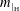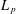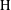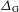Refine listing
Actions for selected content:
423 results in 46Lxx
TRACES ARISING FROM REGULAR INCLUSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 03 November 2016, pp. 190-230
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A remark on fullness of some group measure space von Neumann algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 2493-2502
- Print publication:
- December 2016
-
- Article
- Export citation
Factoriality and Type Classification of k-Graph von Neumann Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 499-518
-
- Article
- Export citation
A CHARACTERISATION OF CENTRAL ELEMENTS IN
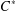 $C^{\ast }$ -ALGEBRAS
$C^{\ast }$ -ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 138-143
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
HAAGERUP PROPERTY FOR
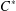 $C^{\ast }$ -CROSSED PRODUCTS
$C^{\ast }$ -CROSSED PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 144-148
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Von Neumann Algebras and Extensions of Inverse Semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 57-97
-
- Article
- Export citation
The Inner Corona Algebra of a C 0(X)-Algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 299-318
-
- Article
- Export citation
FRAMES IN HILBERT C*-MODULES AND MORITA EQUIVALENT C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 03 August 2016, pp. 1-10
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
ADJOINT FUNCTORS BETWEEN CATEGORIES OF HILBERT
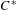 $C^{\ast }$ -MODULES
$C^{\ast }$ -MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 30 June 2016, pp. 453-488
- Print publication:
- April 2018
-
- Article
- Export citation
Schur Multipliers of Cartan Pairs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 413-440
-
- Article
- Export citation
HALF-LIBERATED MANIFOLDS AND THEIR QUANTUM ISOMETRIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 463-492
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
COMPACT ELEMENTS AND OPERATORS OF QUANTUM GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 445-462
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
DUALITIES FOR MAXIMAL COACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 224-254
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
OPERATOR SYSTEM NUCLEARITY VIA
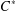 $C^{\ast }$ -ENVELOPES
$C^{\ast }$ -ENVELOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 11 May 2016, pp. 356-375
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Exotic Coactions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 09 March 2016, pp. 411-434
-
- Article
- Export citation
THE LOGARITHMIC FUNCTION AND TRACE ZERO ELEMENTS IN FINITE VON NEUMANN FACTORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 290-295
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Parabolic induction and restriction via
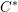 $C^{\ast }$-algebras and Hilbert
$C^{\ast }$-algebras and Hilbert 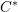 $C^{\ast }$-modules
$C^{\ast }$-modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 1286-1318
- Print publication:
- June 2016
-
- Article
- Export citation
POLISH MODELS AND SOFIC ENTROPY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 18 January 2016, pp. 241-275
- Print publication:
- April 2018
-
- Article
- Export citation
THE NON-COMMUTATIVE KHINTCHINE INEQUALITIES FOR
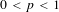 $0<p<1$
$0<p<1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 14 October 2015, pp. 1103-1123
- Print publication:
- November 2017
-
- Article
- Export citation
NONCOMMUTATIVE DE LEEUW THEOREMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 12 October 2015, e21
-
- Article
-
- You have access
- Open access
- Export citation
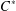
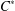
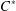
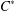
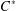
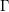
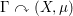
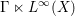
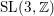
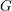
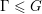
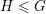
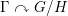
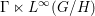
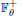 be a single vertex
be a single vertex 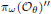 be the von Neumann algebra induced from the Gelfand–Naimark–Segal (GNS) representation of a distinguished state
be the von Neumann algebra induced from the Gelfand–Naimark–Segal (GNS) representation of a distinguished state 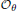 . In this paper we prove the factoriality of
. In this paper we prove the factoriality of 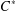
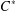
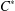
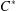
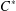
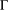
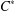
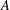

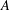


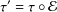
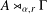
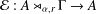
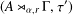
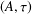
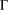
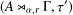
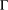
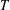
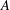
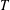
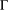
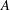
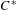
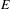
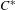

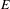
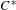
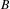
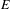
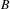

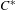
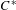
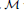 with Cartan maximal abelian self-adjoint algebra
with Cartan maximal abelian self-adjoint algebra 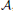 , generalizing the classical Schur multipliers of
, generalizing the classical Schur multipliers of 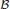 (
(