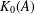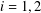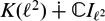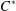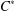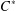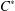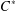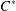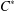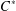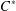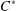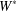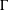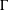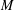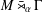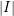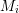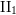Refine listing
Actions for selected content:
423 results in 46Lxx
An Equivariant Theory for the Bivariant Cuntz Semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 573-598
-
- Article
- Export citation
BRANCHING SYSTEMS FOR HIGHER-RANK GRAPH C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 12 March 2018, pp. 731-751
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
A REMARK ON THE TRACIAL ROKHLIN PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 492-498
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
FRAME-LESS HILBERT C*-MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 07 February 2018, pp. 25-31
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
Visualizing Automorphisms of Graph Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 01 February 2018, pp. 215-249
-
- Article
- Export citation
DILATIONS OF INTERACTION GROUPS THAT EXTEND ACTIONS OF ORE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 30 January 2018, pp. 145-161
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
THE STRONG MORITA EQUIVALENCE FOR INCLUSIONS OF
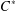 $C^{\ast }$ -ALGEBRAS AND CONDITIONAL EXPECTATIONS FOR EQUIVALENCE BIMODULES
$C^{\ast }$ -ALGEBRAS AND CONDITIONAL EXPECTATIONS FOR EQUIVALENCE BIMODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 12 December 2017, pp. 103-144
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
K-THEORY FOR THE C*-ALGEBRAS OF THE SOLVABLE BAUMSLAG–SOLITAR GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 18 October 2017, pp. 481-486
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
HILBERT C*-BIMODULES OF FINITE INDEX AND APPROXIMATION PROPERTIES OF C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 321-331
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
A stabilization theorem for Fell bundles over groupoids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 79-100
- Print publication:
- February 2018
-
- Article
- Export citation
GRAPH PRODUCTS AND THE ABSENCE OF PROPERTY (AR)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 274-288
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ON GRADED
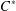 $C^{\ast }$ -ALGEBRAS
$C^{\ast }$ -ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 127-132
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
ON THE ORDER STRUCTURE OF REPRESENTABLE FUNCTIONALS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 289-305
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
WEAK HAAGERUP PROPERTY OF
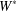 $W^{\ast }$ -CROSSED PRODUCTS
$W^{\ast }$ -CROSSED PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 31 August 2017, pp. 119-126
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
EMBEDDINGS AND
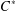 $C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
$C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 274-285
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Numerical Ranges in II1 Factors
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 16 March 2017, pp. 31-55
-
- Article
- Export citation
On the Range Inclusion for Normal Derivations on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 22 February 2017, pp. 1-11
-
- Article
- Export citation
Close hereditary C *-subalgebras and the structure of quasi-multipliers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 263-292
- Print publication:
- April 2017
-
- Article
- Export citation
Cloning in C *-Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 15 December 2016, pp. 689-705
-
- Article
- Export citation
Rigidity of free product von Neumann algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 2461-2492
- Print publication:
- December 2016
-
- Article
- Export citation