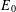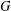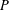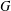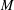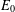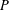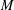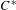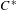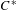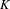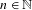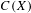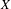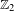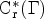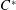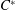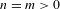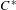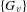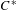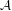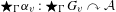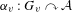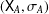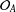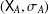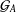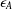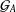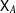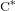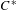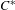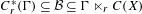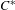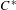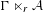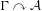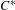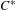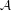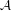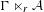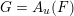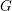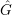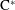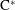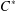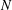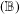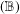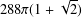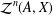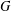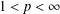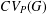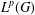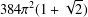Refine listing
Actions for selected content:
423 results in 46Lxx
ARENS PRODUCTS, ARENS REGULARITY AND RELATED PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 138-150
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
MEASURABLE
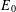 $E_{0}$-SEMIGROUPS ARE CONTINUOUS
$E_{0}$-SEMIGROUPS ARE CONTINUOUS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 04 December 2019, pp. 278-288
- Print publication:
- October 2021
-
- Article
- Export citation
Maximal Inequalities of Noncommutative Martingale Transforms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 221-248
- Print publication:
- February 2021
-
- Article
- Export citation
KMS states on the C*-algebras of Fell bundles over groupoids
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 19 November 2019, pp. 221-246
- Print publication:
- March 2021
-
- Article
- Export citation
Rokhlin dimension: duality, tracial properties, and crossed products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 408-460
- Print publication:
- February 2021
-
- Article
-
- You have access
- Open access
- Export citation
QUANTUM INCREASING SEQUENCES GENERATE QUANTUM PERMUTATION GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 631-639
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
On pathological properties of fixed point algebras in Kirchberg algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 20 September 2019, pp. 3087-3096
- Print publication:
- December 2020
-
- Article
- Export citation
GCR and CCR Steinberg Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1581-1606
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Relations and trails in lattices of projections in W*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1189-1215
-
- Article
- Export citation
M-embedded symmetric operator spaces and the derivation problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 20 August 2019, pp. 607-622
- Print publication:
- November 2020
-
- Article
- Export citation
Finite-dimensional approximations for Nica–Pimsner algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3375-3402
- Print publication:
- December 2020
-
- Article
- Export citation
On graph products of multipliers and the Haagerup property for
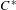 $C^{\ast }$-dynamical systems
$C^{\ast }$-dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 3188-3216
- Print publication:
- December 2020
-
- Article
- Export citation
CUNTZ–KRIEGER ALGEBRAS AND ONE-SIDED CONJUGACY OF SHIFTS OF FINITE TYPE AND THEIR GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 21 June 2019, pp. 289-298
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
CARTAN SUBALGEBRAS IN DIMENSION DROP ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 13 June 2019, pp. 725-755
- Print publication:
- May 2021
-
- Article
-
- You have access
- Open access
- Export citation
Reconstructing directed graphs from generalized gauge actions on their Toeplitz algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 13 June 2019, pp. 2632-2641
- Print publication:
- October 2020
-
- Article
- Export citation
On simplicity of intermediate
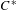 $C^{\ast }$-algebras
$C^{\ast }$-algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 3181-3187
- Print publication:
- December 2020
-
- Article
- Export citation
Martin boundaries of the duals of free unitary quantum groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 31 May 2019, pp. 1171-1193
- Print publication:
- June 2019
-
- Article
- Export citation
Corrigendum to: A Galois Correspondence for Reduced Crossed Products of Simple
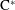 $\text{C}^{\ast }$-algebras by Discrete Groups
$\text{C}^{\ast }$-algebras by Discrete Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 May 2019, pp. 557-562
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
HOMOLOGY AND MATUI’S HK CONJECTURE FOR GROUPOIDS ON ONE-DIMENSIONAL SOLENOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 105-117
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
HYPERREFLEXIVITY CONSTANTS OF THE BOUNDED
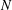 $N$-COCYCLE SPACES OF GROUP ALGEBRAS AND C*-ALGEBRAS
$N$-COCYCLE SPACES OF GROUP ALGEBRAS AND C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 30 April 2019, pp. 112-130
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation