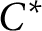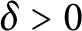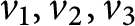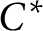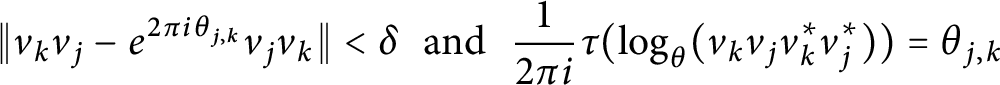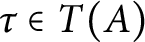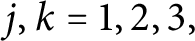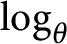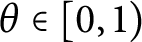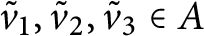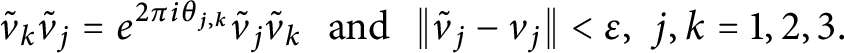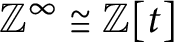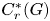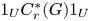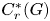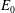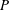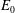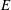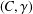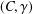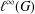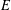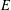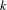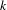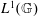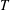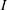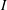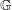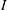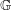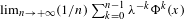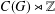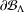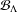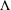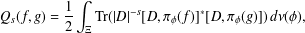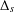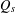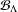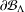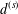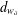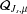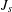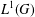Refine listing
Actions for selected content:
424 results in 46Lxx
Stability of rotation relations in
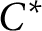 $C^*$-algebras
$C^*$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 21 May 2020, pp. 1171-1203
- Print publication:
- August 2021
-
- Article
- Export citation
Dimension groups for self-similar maps and matrix representations of the cores of the associated C*-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 1013-1056
- Print publication:
- August 2021
-
- Article
- Export citation
Dynamics of compact quantum metric spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 11 May 2020, pp. 2069-2109
- Print publication:
- July 2021
-
- Article
- Export citation
A generalized type semigroup and dynamical comparison
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 2148-2165
- Print publication:
- July 2021
-
- Article
- Export citation
Edwards' condition for quasitraces on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 525-547
- Print publication:
- April 2021
-
- Article
-
- You have access
- Open access
- Export citation
QUOTIENTS OF ÉTALE GROUPOIDS AND THE ABELIANIZATIONS OF GROUPOID C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 07 April 2020, pp. 56-75
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
Dense subalgebras of purely infinite simple groupoid C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 30 March 2020, pp. 609-629
-
- Article
- Export citation
INDUCTIVE LIMITS OF C*-ALGEBRAS AND COMPACT QUANTUM METRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 27 March 2020, pp. 289-312
- Print publication:
- December 2021
-
- Article
- Export citation
Measurable and Continuous Units of an
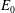 $E_{0}$-semigroup
$E_{0}$-semigroup
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 25 March 2020, pp. 469-478
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
TENSOR-PRODUCT COACTION FUNCTORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 March 2020, pp. 52-67
- Print publication:
- February 2022
-
- Article
- Export citation
SIMPLICITY OF TWISTED C*-ALGEBRAS OF TOPOLOGICAL HIGHER-RANK GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 512-513
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
RECOVERING THE BOUNDARY PATH SPACE OF A TOPOLOGICAL GRAPH USING POINTLESS TOPOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 232-248
- Print publication:
- October 2021
-
- Article
- Export citation
C*-algebras of a Cantor system with finitely many minimal subsets: structures, K-theories, and the index map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1296-1341
- Print publication:
- May 2021
-
- Article
- Export citation
Free minimal actions of countable groups with invariant probability measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1369-1389
- Print publication:
- May 2021
-
- Article
- Export citation
Ideals of the Quantum Group Algebra, Arens Regularity and Weakly Compact Multipliers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 825-836
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Matrix Liberation Process II: Relation to Orbital Free Entropy
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 493-541
- Print publication:
- April 2021
-
- Article
- Export citation
Ergodic properties of the Anzai skew-product for the non-commutative torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1064-1085
- Print publication:
- April 2021
-
- Article
- Export citation
UNBOUNDED DERIVATIONS IN ALGEBRAS ASSOCIATED WITH MONOTHETIC GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 345-371
- Print publication:
- December 2021
-
- Article
- Export citation
DIRICHLET FORMS AND ULTRAMETRIC CANTOR SETS ASSOCIATED TO HIGHER-RANK GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 194-219
- Print publication:
- April 2021
-
- Article
- Export citation
ZERO JORDAN PRODUCT DETERMINED BANACH ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 145-158
- Print publication:
- October 2021
-
- Article
- Export citation