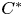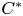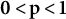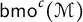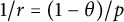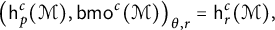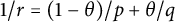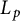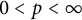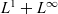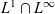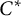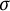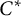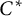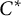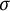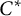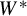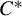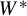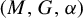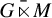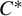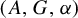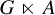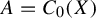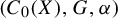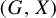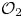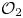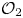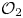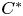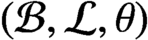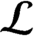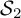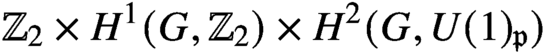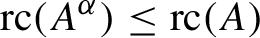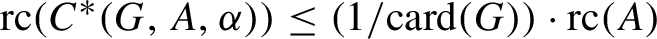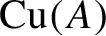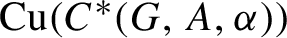Refine listing
Actions for selected content:
422 results in 46Lxx
Invariance of KMS states on graph C*-algebras under classical and quantum symmetry
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 20 September 2021, pp. 762-778
-
- Article
- Export citation
Wick polynomials in noncommutative probability: a group-theoretical approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 1673-1699
- Print publication:
- December 2022
-
- Article
- Export citation
Interpolation between noncommutative martingale Hardy and BMO spaces: the case
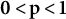 $\textbf {0<p<1}$
$\textbf {0<p<1}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 1700-1744
- Print publication:
- December 2022
-
- Article
- Export citation
C*-algebras where every element is a limit of products of positive elements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 628-632
- Print publication:
- September 2022
-
- Article
- Export citation
EXTREME POINT METHODS IN THE STUDY OF ISOMETRIES ON CERTAIN NONCOMMUTATIVE SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 462-483
- Print publication:
- May 2022
-
- Article
- Export citation
APPROXIMATELY MULTIPLICATIVE DECOMPOSITIONS OF NUCLEAR MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 26 July 2021, pp. 314-322
- Print publication:
- April 2022
-
- Article
- Export citation
A GENERALISATION OF HIGHER-RANK GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 26 July 2021, pp. 257-266
- Print publication:
- April 2022
-
- Article
- Export citation
Uniformly quasi-Hermitian groups are supramenable
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 July 2021, pp. 665-673
- Print publication:
- September 2022
-
- Article
- Export citation
The Picard groups of inclusions of
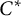 $C^*$-algebras induced by equivalence bimodules
$C^*$-algebras induced by equivalence bimodules
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 743-758
- Print publication:
- September 2022
-
- Article
- Export citation
Amenable dynamical systems over locally compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 25 June 2021, pp. 2468-2508
- Print publication:
- August 2022
-
- Article
- Export citation
Equivariant
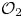 $\mathcal {O}_{2}$-absorption theorem for exact groups
$\mathcal {O}_{2}$-absorption theorem for exact groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 17 June 2021, pp. 1492-1506
- Print publication:
- July 2021
-
- Article
- Export citation
Operator equalities and Characterizations of Orthogonality in Pre-Hilbert C*-Modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 17 June 2021, pp. 594-614
-
- Article
- Export citation
Homology and K-theory of dynamical systems I. Torsion-free ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 2630-2660
- Print publication:
- August 2022
-
- Article
- Export citation
CONDITION (K) FOR BOOLEAN DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 145-169
- Print publication:
- April 2022
-
- Article
- Export citation
On one-sided topological conjugacy of topological Markov shifts and gauge actions on Cuntz–Krieger algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 2575-2582
- Print publication:
- August 2022
-
- Article
- Export citation
Regularity of simple nuclear real C*-algebras under tracial conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 139-147
-
- Article
- Export citation
RIESZ TRANSFORMS ON COMPACT QUANTUM GROUPS AND STRONG SOLIDITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 2135-2171
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
INVARIANT SETS AND NORMAL SUBGROUPOIDS OF UNIVERSAL ÉTALE GROUPOIDS INDUCED BY CONGRUENCES OF INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 April 2021, pp. 99-118
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- Export citation
The classification of symmetry protected topological phases of one-dimensional fermion systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 16 March 2021, e25
-
- Article
-
- You have access
- Open access
- Export citation
The Cuntz semigroup and the radius of comparison of the crossed product by a finite group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 10 March 2021, pp. 3541-3592
- Print publication:
- December 2021
-
- Article
- Export citation