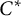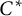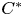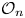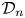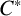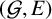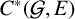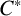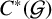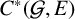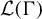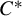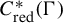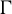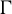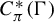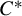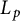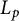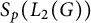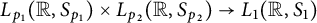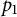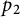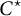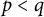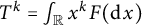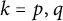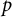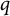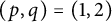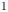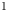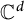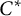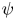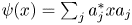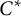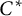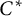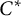Refine listing
Actions for selected content:
422 results in 46Lxx
A note on the nuclear dimension of Cuntz–Pimsner
 $C^*$-algebras associated with minimal shift spaces
$C^*$-algebras associated with minimal shift spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 12 December 2022, pp. 104-125
- Print publication:
- February 2024
-
- Article
- Export citation
Colored isomorphism of classifiable C
 $^*$-algebras
$^*$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 12 December 2022, pp. 216-245
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On conjugacy of subalgebras in graph C*-algebras. II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1162-1182
-
- Article
- Export citation
Double relative commutants in coronas of separable C*-algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 345-355
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
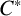 $C^*$-ALGEBRAS OF SELF-SIMILAR ACTION OF GROUPOIDS ON ROW-FINITE DIRECTED GRAPHS
$C^*$-ALGEBRAS OF SELF-SIMILAR ACTION OF GROUPOIDS ON ROW-FINITE DIRECTED GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 150-161
- Print publication:
- August 2023
-
- Article
- Export citation
On invariant subalgebras of group
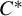 $C^*$ and von Neumann algebras
$C^*$ and von Neumann algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 3341-3353
- Print publication:
- October 2023
-
- Article
- Export citation
Multilinear transference of Fourier and Schur multipliers acting on noncommutative
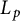 $L_p$-spaces
$L_p$-spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 1986-2006
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A multiplicative Kowalski–Słodkowski theorem for
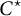 $C^\star $-algebras
$C^\star $-algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 02 November 2022, pp. 951-958
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Cuntz semigroup of unital commutative AI-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 1831-1868
- Print publication:
- December 2023
-
- Article
- Export citation
A polynomial approximation result for free Herglotz–Agler functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 665-678
- Print publication:
- June 2023
-
- Article
- Export citation
A correspondence between inverse subsemigroups, open wide subgroupoids and cartan intermediate C*-subalgebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 October 2022, pp. 861-879
-
- Article
- Export citation
Spectra of infinite graphs via freeness with amalgamation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1633-1684
- Print publication:
- October 2023
-
- Article
- Export citation
Examples of multiparameter CCR flows with non-trivial index
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 27 September 2022, pp. 799-832
-
- Article
- Export citation
The isomorphism problem for tensor algebras of multivariable dynamical systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 19 September 2022, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two-moment characterization of spectral measures on the real line
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 1369-1392
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conjugacy of local homeomorphisms via groupoids and C*-algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 18 August 2022, pp. 2516-2537
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poisson boundaries of II1 factors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 October 2022, pp. 1746-1776
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noncommutative rational Clark measures
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 27 July 2022, pp. 1393-1445
- Print publication:
- October 2023
-
- Article
- Export citation
Which states can be reached from a given state by unital completely positive maps?
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 05 July 2022, pp. 632-651
-
- Article
- Export citation
The generator rank of subhomogeneous
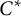 $C^*\!$-algebras
$C^*\!$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1314-1342
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation