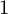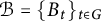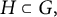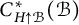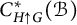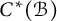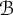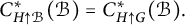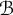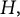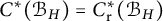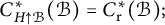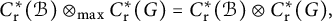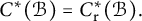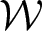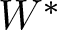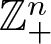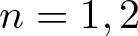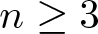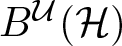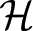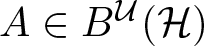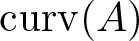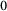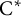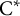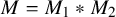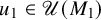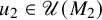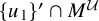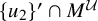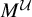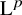Refine listing
Actions for selected content:
422 results in 46Lxx
Products of commutators in matrix rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 512-529
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 366-379
- Print publication:
- October 2025
-
- Article
- Export citation
On multiparameter CAR (canonical anticommutation relation) flows
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-37
-
- Article
- Export citation
PRIMITIVE IDEAL SPACE OF
 $C^*(R_+)\rtimes R^\times $
$C^*(R_+)\rtimes R^\times $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 345-354
- Print publication:
- October 2025
-
- Article
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
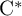 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cross-sectional C*-algebras associated with subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2024, pp. 1-26
-
- Article
- Export citation
Crossed products as compact quantum metric spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2024, pp. 1-31
-
- Article
- Export citation
Central Limit Theorem for tensor products of free variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-33
-
- Article
- Export citation
Strongly outer actions of certain torsion-free amenable groups on the Razak–Jacelon algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transference of multilinear Fourier and Schur multipliers acting on noncommutative
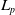 $L_p$-spaces for non-unimodular groups
$L_p$-spaces for non-unimodular groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 197-223
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical invariants on twisted noncommutative polyballs: curvature and multiplicity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-54
-
- Article
- Export citation
The admissible KMS bundles on classifiable C⁎-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 117-156
- Print publication:
- January 2025
-
- Article
- Export citation
Some Fock spaces with depth two action
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 05 November 2024, pp. 1890-1918
- Print publication:
- December 2025
-
- Article
- Export citation
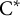 $\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
$\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 November 2024, pp. 1081-1091
- Print publication:
- December 2024
-
- Article
- Export citation
Asymptotic freeness in tracial ultraproducts
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE EVANS CHAIN COMPLEX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 552-562
- Print publication:
- June 2025
-
- Article
- Export citation
Haagerup and Størmer's conjecture on pointwise inner automorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 04 November 2024, pp. 2480-2495
- Print publication:
- October 2024
-
- Article
- Export citation
CUNTZ–KRIEGER ALGEBRAS ASSOCIATED TO SELF-SIMILAR GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 27 September 2024, pp. 568-569
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation