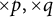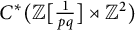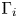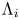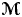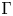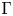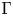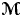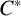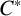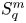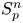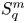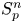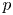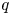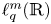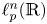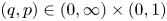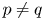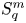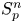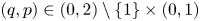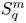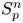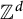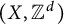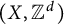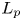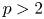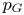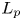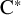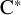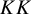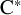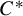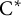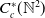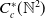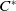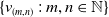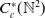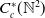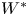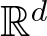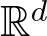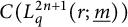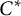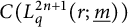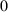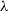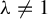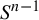Refine listing
Actions for selected content:
422 results in 46Lxx
A tracial characterization of Furstenberg’s
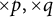 $\times p,\times q$ conjecture
$\times p,\times q$ conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 06 September 2023, pp. 244-256
- Print publication:
- March 2024
-
- Article
- Export citation
Corrigendum: Von Neumann algebras and extensions of inverse semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 919-922
-
- Article
-
- You have access
- HTML
- Export citation
Measure equivalence rigidity via s-malleable deformations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 14 August 2023, pp. 2023-2050
- Print publication:
- October 2023
-
- Article
- Export citation
ON POSSIBLE VALUES OF THE INTERIOR ANGLE BETWEEN INTERMEDIATE SUBALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 44-66
- Print publication:
- August 2024
-
- Article
- Export citation
A NATURAL DEDUCTION SYSTEM FOR ORTHOMODULAR LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 910-949
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On isometric embeddability of $S_q^m$
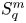 into $S_p^n$
into $S_p^n$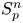 as non-commutative quasi-Banach spaces
as non-commutative quasi-Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 June 2023, pp. 1180-1203
- Print publication:
- August 2024
-
- Article
- Export citation
Radius of comparison and mean topological dimension:
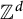 $\mathbb Z^d$-actions
$\mathbb Z^d$-actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 1240-1266
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bi-free entropy with respect to completely positive maps
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1163-1239
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric actions on Lp-spaces: dependence on the value of p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1300-1313
- Print publication:
- June 2023
-
- Article
- Export citation
Chaotic tracial dynamics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 May 2023, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTABLE PRESENTATIONS OF C*-ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1313-1338
- Print publication:
- September 2024
-
- Article
- Export citation
Binary factors of shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 888-932
- Print publication:
- March 2024
-
- Article
- Export citation
Random amenable C*-algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 345-366
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dilations of Markovian semigroups of measurable Schur multipliers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 774-797
- Print publication:
- June 2024
-
- Article
- Export citation
On tracial
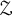 ${\mathcal {Z}}$-stability of simple non-unital
${\mathcal {Z}}$-stability of simple non-unital 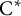 $\mathrm {C}^*$-algebras
$\mathrm {C}^*$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KMS states on
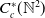 $C_c^{*}(\mathbb{N}^2)$
$C_c^{*}(\mathbb{N}^2)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 501-528
- Print publication:
- September 2023
-
- Article
- Export citation
Orbit equivalence rigidity of irreducible actions of right-angled Artin groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 860-887
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decomposability of multiparameter car flows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 March 2023, pp. 1-22
-
- Article
- Export citation
On the classification and description of quantum lens spaces as graph algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 25 January 2023, pp. 246-282
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orbit equivalence superrigidity for type III
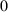 $_0$ actions
$_0$ actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 4193-4225
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation