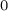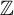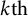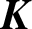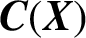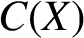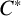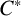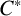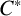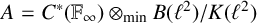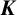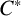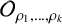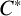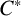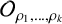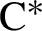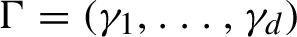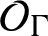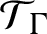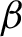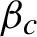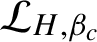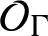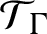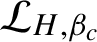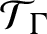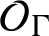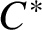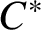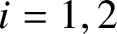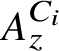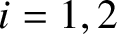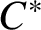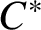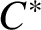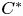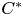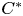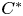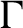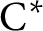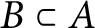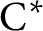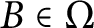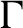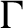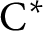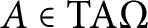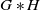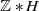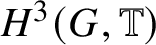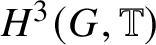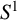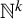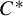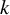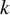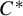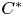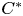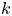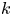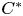Refine listing
Actions for selected content:
422 results in 46Lxx
BERNOULLI ACTIONS OF TYPE III
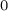 $_0$ WITH PRESCRIBED ASSOCIATED FLOW
$_0$ WITH PRESCRIBED ASSOCIATED FLOW
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 14 June 2022, pp. 71-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Operator noncommutative functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 492-508
- Print publication:
- June 2023
-
- Article
- Export citation
RATIONAL
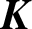 $\boldsymbol {K}$-STABILITY OF CONTINUOUS
$\boldsymbol {K}$-STABILITY OF CONTINUOUS 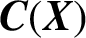 $\boldsymbol {C(X)}$-ALGEBRAS
$\boldsymbol {C(X)}$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 119-144
- Print publication:
- August 2023
-
- Article
- Export citation
ON
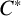 $\mathbf{\mathit{C}}^{*}$-ALGEBRAS WHICH DETECT NUCLEARITY
$\mathbf{\mathit{C}}^{*}$-ALGEBRAS WHICH DETECT NUCLEARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 May 2022, pp. 125-133
- Print publication:
- February 2023
-
- Article
- Export citation
A counterexample to the HK-conjecture that is principal
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1829-1846
- Print publication:
- June 2023
-
- Article
- Export citation
Left regular representations of Garside categories I. C*-algebras and groupoids
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. S53-S86
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REPRESENTING STRUCTURED SEMIGROUPS ON ÉTALE GROUPOID BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1-49
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
C
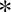 $^{\ast }$-simplicity has no local obstruction
$^{\ast }$-simplicity has no local obstruction
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 March 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
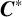 $\boldsymbol {C}^{*}$-ALGEBRAS FROM
$\boldsymbol {C}^{*}$-ALGEBRAS FROM 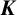 $\boldsymbol {K}$ GROUP REPRESENTATIONS
$\boldsymbol {K}$ GROUP REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 318-338
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KMS states for generalized gauge actions on
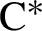 $\mathrm {C}^{\ast }$-algebras associated with self-similar sets
$\mathrm {C}^{\ast }$-algebras associated with self-similar sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 01 March 2022, pp. 1222-1238
- Print publication:
- April 2023
-
- Article
- Export citation
Nonamenable simple
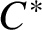 $C^*$-algebras with tracial approximation
$C^*$-algebras with tracial approximation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 February 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strong morita equivalence for conditional expectations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 182-213
-
- Article
- Export citation
Exact structures for operator modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 421-446
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform property
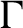 $\Gamma $ for certain
$\Gamma $ for certain 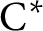 $\mathrm {C^*}$-algebras
$\mathrm {C^*}$-algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1063-1070
- Print publication:
- December 2022
-
- Article
- Export citation
Weak amenability of free products of hyperbolic and amenable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 698-701
- Print publication:
- September 2022
-
- Article
- Export citation
An
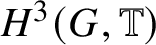 $H^{3}(G,{\mathbb T})$-valued index of symmetry-protected topological phases with on-site finite group symmetry for two-dimensional quantum spin systems
$H^{3}(G,{\mathbb T})$-valued index of symmetry-protected topological phases with on-site finite group symmetry for two-dimensional quantum spin systems
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 16 December 2021, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A few remarks on Pimsner–Popa bases and regular subfactors of depth 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 01 December 2021, pp. 586-602
- Print publication:
- September 2022
-
- Article
- Export citation
RELATIVELY AMENABLE ACTIONS OF THOMPSON’S GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 03 November 2021, pp. 144-150
- Print publication:
- August 2022
-
- Article
- Export citation
Cocycles on groupoids arising from
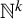 $\mathbb {N}^k$-actions
$\mathbb {N}^k$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3325-3356
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure theory and stable rank for C*-algebras of finite higher-rank graphs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 04 October 2021, pp. 822-847
-
- Article
- Export citation