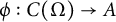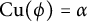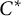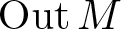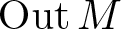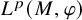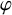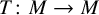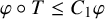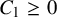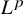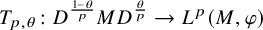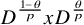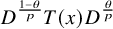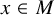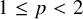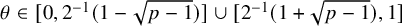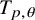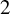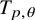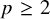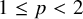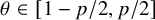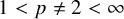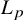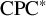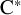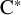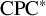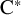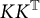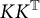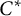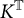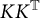Refine listing
Actions for selected content:
424 results in 46Lxx
CORONA RIGIDITY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 195-287
- Print publication:
- June 2025
-
- Article
- Export citation
Cartesian closed varieties II: links to algebra and self-similarity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2025, pp. 1-45
-
- Article
- Export citation
On Fock covariance for product systems and the reduced Hao–Ng isomorphism problem by discrete actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-53
-
- Article
- Export citation
Classification of homomorphisms from
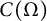 $C(\Omega)$ to a
$C(\Omega)$ to a 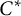 $C^*$-algebra
$C^*$-algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1-24
-
- Article
- Export citation
Every locally compact group is the outer automorphism group of a II1 factor
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1-12
-
- Article
- Export citation
On the extension of positive maps to Haagerup noncommutative
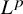 $L^p$-spaces
$L^p$-spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 March 2025, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The local geometry of idempotent Schur multipliers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nuclearity and
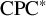 ${\mathrm {CPC}^*}$-Systems
${\mathrm {CPC}^*}$-Systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 March 2025, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLICATIVE (IN)STABILITY OF BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 194-200
- Print publication:
- August 2025
-
- Article
- Export citation
Moments of the free Jacobi process: A matrix approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 966-991
- Print publication:
- September 2025
-
- Article
- Export citation
Non-commutative skew-product extension dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2672-2694
- Print publication:
- September 2025
-
- Article
- Export citation
RELATIVE POSITION BETWEEN A PAIR OF SPIN MODEL SUBFACTORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-38
- Print publication:
- August 2025
-
- Article
- Export citation
Uniform property
 $ \Gamma $ and finite dimensional tracial boundaries
$ \Gamma $ and finite dimensional tracial boundaries
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 March 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KK-theory of circle actions with the Rokhlin property
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute dilations of UCP self-adjoint Fourier multipliers: the nonunimodular case
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 307-324
- Print publication:
- September 2025
-
- Article
- Export citation
The lattice of C
 $^*$-covers of an operator algebra
$^*$-covers of an operator algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The imprimitivity Fell bundle
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-44
-
- Article
- Export citation
Extending surjective maps preserving the norm of symmetric Kubo-Ando means
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 777-786
- Print publication:
- September 2025
-
- Article
- Export citation
Large N limit of the Yang–Mills measure on compact surfaces II: Makeenko–Migdal equations and the planar master field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation




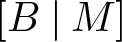
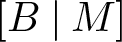
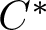
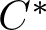
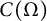
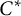

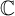
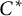
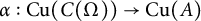
 , there exists a homomorphism
, there exists a homomorphism