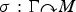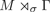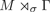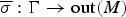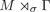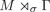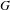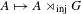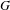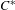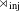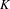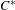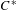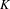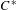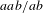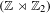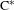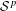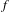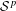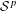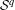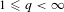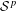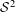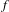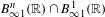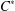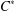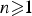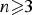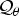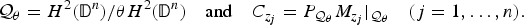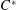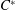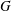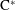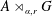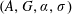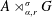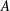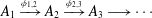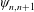Refine listing
Actions for selected content:
423 results in 46Lxx
Fullness of crossed products of factors by discrete groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 23 April 2019, pp. 2368-2378
- Print publication:
- October 2020
-
- Article
- Export citation
The maximal injective crossed product
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 22 April 2019, pp. 2995-3014
- Print publication:
- November 2020
-
- Article
-
- You have access
- Open access
- Export citation
Equilibrium states on higher-rank Toeplitz non-commutative solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 April 2019, pp. 2881-2912
- Print publication:
- November 2020
-
- Article
- Export citation
The stable algebra of a Wieler solenoid: inductive limits and
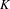 $K$ -theory
$K$ -theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 10 April 2019, pp. 2734-2768
- Print publication:
- October 2020
-
- Article
- Export citation
SIMPLICITY OF CROSSED PRODUCTS BY TWISTED PARTIAL ACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 202-225
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Heisenberg Modules over Quantum 2-tori are Metrized Quantum Vector Bundles
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 28 March 2019, pp. 1044-1081
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Homology of odometers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 13 March 2019, pp. 2541-2551
- Print publication:
- September 2020
-
- Article
- Export citation
THE UNITAL EXT-GROUPS AND CLASSIFICATION OF C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 13 March 2019, pp. 201-231
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
ENFORCEABLE OPERATOR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 01 March 2019, pp. 31-63
- Print publication:
- January 2021
-
- Article
-
- You have access
- Export citation
HIGHER ORDER DIFFERENTIABILITY OF OPERATOR FUNCTIONS IN SCHATTEN NORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 13 February 2019, pp. 1993-2016
- Print publication:
- November 2020
-
- Article
- Export citation
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On quotient modules of H2(𝔻n): essential normality and boundary representations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 1339-1359
- Print publication:
- June 2020
-
- Article
- Export citation
Induction for locally compact quantum groups revisited
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1071-1093
- Print publication:
- April 2020
-
- Article
- Export citation
Factoriality, Connes' type III invariants and fullness of amalgamated free product von Neumann algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1495-1532
- Print publication:
- June 2020
-
- Article
- Export citation
Freeness and The Partial Transposes of Wishart Random Matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 659-681
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Elements of
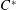 $C^{\ast }$-algebras Attaining their Norm in a Finite-dimensional Representation
$C^{\ast }$-algebras Attaining their Norm in a Finite-dimensional Representation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 93-111
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Asymptotic Continuous Orbit Equivalence of Smale Spaces and Ruelle Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1243-1296
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A Galois Correspondence for Reduced Crossed Products of Simple
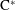 $\text{C}^{\ast }$-algebras by Discrete Groups
$\text{C}^{\ast }$-algebras by Discrete Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1103-1125
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Injectivity of the Connecting Homomorphisms in Inductive Limits of Elliott–Thomsen Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 131-148
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Spectral Flow Argument Localizing an Odd Index Pairing
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 373-381
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation