Refine listing
Actions for selected content:
423 results in 46Lxx
Integral Formula for Spectral Flow for
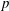 $p$-Summable Operators
$p$-Summable Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 337-379
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Boundary Quotient
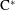 $\text{C}^{\ast }$-algebras of Products of Odometers
$\text{C}^{\ast }$-algebras of Products of Odometers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 183-212
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF TRACIALLY NUCLEAR C*-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 119-128
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A proof of Boca's Theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 869-876
- Print publication:
- August 2019
-
- Article
- Export citation
A VON NEUMANN ALGEBRA CHARACTERIZATION OF PROPERTY (T) FOR GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 363-386
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
FACTORISATION OF EQUIVARIANT SPECTRAL TRIPLES IN UNBOUNDED
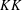 $KK$-THEORY
$KK$-THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 145-180
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Amenable purely infinite actions on the non-compact Cantor set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1619-1633
- Print publication:
- June 2020
-
- Article
- Export citation
Rigid C*-Tensor Categories and their Realizations as Hilbert C*-Bimodules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 367-393
-
- Article
- Export citation
Delone dynamical systems and spectral convergence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 22 October 2018, pp. 1510-1544
- Print publication:
- June 2020
-
- Article
- Export citation
LIBERATION, FREE MUTUAL INFORMATION AND ORBITAL FREE ENTROPY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 14 September 2018, pp. 205-231
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Monic representations of finite higher-rank graphs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 06 September 2018, pp. 1238-1267
- Print publication:
- May 2020
-
- Article
- Export citation
LEFT SYMMETRIC POINTS FOR BIRKHOFF ORTHOGONALITY IN THE PREDUALSOF VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 494-501
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Stability of products of equivalence relations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 2005-2019
- Print publication:
- September 2018
-
- Article
- Export citation
Subgroup Correspondences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 14 August 2018, pp. 1127-1154
-
- Article
- Export citation
A dichotomy for groupoid
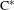 $\text{C}^{\ast }$-algebras
$\text{C}^{\ast }$-algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 13 August 2018, pp. 521-563
- Print publication:
- February 2020
-
- Article
- Export citation
ON FUNDAMENTAL GROUPS OF TENSOR PRODUCT
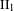 $\text{II}_{1}$ FACTORS
$\text{II}_{1}$ FACTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 02 August 2018, pp. 1121-1139
- Print publication:
- July 2020
-
- Article
- Export citation
Andô dilations and inequalities on non-commutative domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 06 July 2018, pp. 1239-1267
- Print publication:
- December 2018
-
- Article
- Export citation
A Few Remarks on the Tube Algebra of a Monoidal Category
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 08 May 2018, pp. 735-758
-
- Article
- Export citation
Perforation conditions and almost algebraic order in Cuntz semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 669-702
- Print publication:
- August 2018
-
- Article
- Export citation
Ulam stability for some classes of C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 10 April 2018, pp. 45-59
- Print publication:
- February 2019
-
- Article
- Export citation
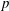
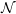

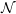
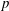
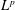
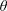
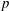
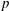
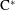
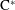
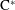
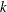
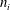
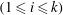
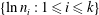
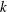
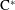
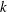
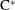
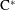
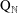
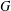
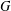
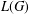
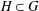
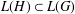
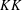
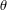
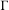
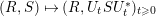
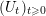
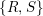
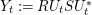
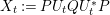
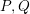
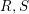
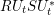
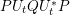
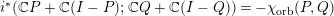
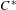
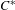
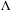
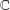
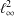
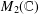
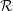
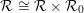
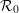
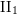
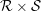
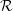
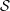
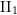
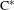

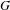

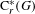
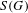

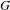
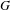
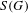
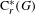
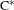
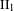
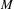
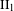
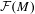
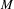
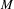
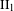
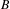
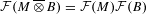
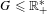
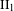
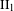
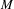
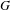
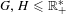
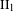
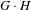
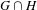
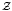 ) in terms of Cu(
) in terms of Cu(