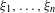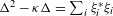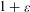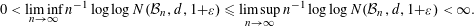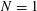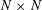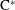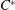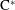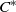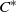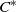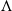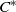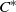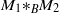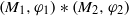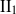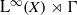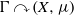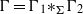Refine listing
Actions for selected content:
423 results in 46Lxx
ERGODIC EXTENSIONS OF ENDOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 02 October 2015, pp. 307-320
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF 3-JORDAN HOMOMORPHISMS ON BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 04 September 2015, pp. 301-306
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
GROUP ACTION PRESERVING THE HAAGERUP PROPERTY OF
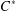 $C^{\ast }$-ALGEBRAS
$C^{\ast }$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 August 2015, pp. 295-300
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
A CONTINUUM OF C*-NORMS ON
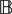 ${\mathbb B}$(H) ⊗
${\mathbb B}$(H) ⊗ 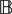 ${\mathbb B}$(H) AND RELATED TENSOR PRODUCTS
${\mathbb B}$(H) AND RELATED TENSOR PRODUCTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 22 July 2015, pp. 433-443
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
LEBESGUE DECOMPOSITION FOR REPRESENTABLE FUNCTIONALS ON *-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 491-501
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
REMARKS ON
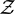 ${\mathcal{Z}}$-STABLE PROJECTIONLESS C*-ALGEBRAS
${\mathcal{Z}}$-STABLE PROJECTIONLESS C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 273-277
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
FREDHOLM MODULES OVER GRAPH
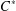 $C^{\ast }$-ALGEBRAS
$C^{\ast }$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 19 June 2015, pp. 302-315
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
DERIVATIONS OF FRÉCHET NUCLEAR GB
 $^{\ast }$-ALGEBRAS
$^{\ast }$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 04 June 2015, pp. 290-301
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
SMOOTH BIMODULES AND COHOMOLOGY OF II1 FACTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 07 May 2015, pp. 155-187
- Print publication:
- February 2017
-
- Article
- Export citation
PERIODIC
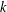 $k$-GRAPH ALGEBRAS REVISITED
$k$-GRAPH ALGEBRAS REVISITED
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 20 April 2015, pp. 267-286
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
QUOTIENT AND PSEUDO UNIT IN NONUNITAL OPERATOR SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 123-132
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
TWISTED TOPOLOGICAL GRAPH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 514-515
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Classifying Polygonal Algebras by their K0-Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 13 February 2015, pp. 485-497
-
- Article
-
- You have access
- Export citation
DIRECTLY FINITE ALGEBRAS OF PSEUDOFUNCTIONS ON LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 693-707
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
NONCOMMUTATIVE REAL ALGEBRAIC GEOMETRY OF KAZHDAN’S PROPERTY (T)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 30 July 2014, pp. 85-90
- Print publication:
- January 2016
-
- Article
- Export citation
RIGIDITY OF CONTINUOUS QUOTIENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2014, pp. 1-28
- Print publication:
- January 2016
-
- Article
- Export citation
ON THE METRIC ENTROPY OF THE BANACH–MAZUR COMPACTUM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 May 2014, pp. 179-198
- Print publication:
- January 2015
-
- Article
- Export citation
A NONSEPARABLE AMENABLE OPERATOR ALGEBRA WHICH IS NOT ISOMORPHIC TO A
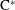 $C^*$ -ALGEBRA
$C^*$ -ALGEBRA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 March 2014, e2
-
- Article
-
- You have access
- Open access
- Export citation
JOINS AND COVERS IN INVERSE SEMIGROUPS AND TIGHT
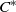 ${C}^{\ast } $-ALGEBRAS
${C}^{\ast } $-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 121-133
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Amalgamated free product type III factors with at most one Cartan subalgebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 13 December 2013, pp. 143-174
- Print publication:
- January 2014
-
- Article
- Export citation
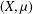
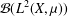
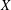
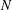

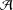
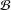
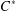
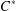
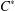
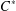
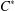
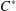
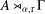
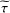
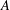

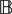
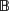
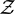
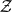
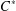
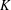
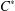
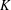
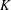


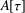
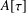



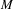
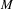
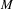
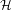
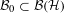
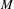
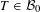

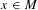
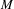
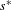
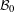
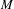
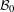
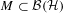
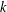
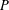
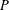
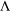
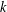
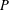
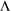
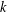
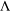
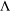
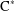
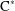
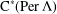
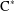
 of the identity in
of the identity in